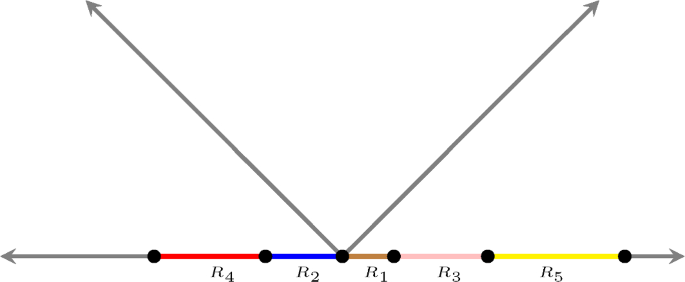
Solution to the n-bubble problem on \(\mathbb {R}^1\) with log-concave density

We study the n-bubble problem on \(\mathbb {R}^1\) with a prescribed density function f that is even, radially increasing, and satisfies a log-concavity requirement. Under these conditions, we find that isoperimetric solutions can be identified for an arbitrary number of regions, and that these solutions have a well-understood and regular structure. This generalizes recent work done on the density function \(|x |^p\) and stands in contrast to log-convex density functions which are known to have no such regular structure.