球上$\mathrm {PU}(p)$ -束规范群的同伦类型

IF 0.5 4区数学

Journal of Homotopy and Related Structures Pub Date : 2021-01-21 DOI:10.1007/s40062-020-00274-0

Simon Rea

{"title":"球上\$\\mathrm {PU}(p)\$ -束规范群的同伦类型","authors":"Simon Rea","doi":"10.1007/s40062-020-00274-0","DOIUrl":null,"url":null,"abstract":"We examine the relation between the gauge groups of \$\\mathrm {SU}(n)\$- and \$\\mathrm {PU}(n)\$-bundles over \$S^{2i}\$, with \$2\\le i\\le n\$, particularly when n is a prime. As special cases, for \$\\mathrm {PU}(5)\$-bundles over \$S^4\$, we show that there is a rational or p-local equivalence \$\\mathcal {G}_{2,k}\\simeq _{(p)}\\mathcal {G}_{2,l}\$ for any prime p if, and only if, \$(120,k)=(120,l)\$, while for \$\\mathrm {PU}(3)\$-bundles over \$S^6\$ there is an integral equivalence \$\\mathcal {G}_{3,k}\\simeq \\mathcal {G}_{3,l}\$ if, and only if, \$(120,k)=(120,l)\$.","PeriodicalId":636,"journal":{"name":"Journal of Homotopy and Related Structures","volume":"16 1","pages":"61 - 74"},"PeriodicalIF":0.5000,"publicationDate":"2021-01-21","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"https://sci-hub-pdf.com/10.1007/s40062-020-00274-0","citationCount":"2","resultStr":"{\"title\":\"Homotopy types of gauge groups of \\\$\\\\mathrm {PU}(p)\\\$-bundles over spheres\",\"authors\":\"Simon Rea\",\"doi\":\"10.1007/s40062-020-00274-0\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"We examine the relation between the gauge groups of \\\$\\\\mathrm {SU}(n)\\\$- and \\\$\\\\mathrm {PU}(n)\\\$-bundles over \\\$S^{2i}\\\$, with \\\$2\\\\le i\\\\le n\\\$, particularly when n is a prime. As special cases, for \\\$\\\\mathrm {PU}(5)\\\$-bundles over \\\$S^4\\\$, we show that there is a rational or p-local equivalence \\\$\\\\mathcal {G}_{2,k}\\\\simeq _{(p)}\\\\mathcal {G}_{2,l}\\\$ for any prime p if, and only if, \\\$(120,k)=(120,l)\\\$, while for \\\$\\\\mathrm {PU}(3)\\\$-bundles over \\\$S^6\\\$ there is an integral equivalence \\\$\\\\mathcal {G}_{3,k}\\\\simeq \\\\mathcal {G}_{3,l}\\\$ if, and only if, \\\$(120,k)=(120,l)\\\$.\",\"PeriodicalId\":636,\"journal\":{\"name\":\"Journal of Homotopy and Related Structures\",\"volume\":\"16 1\",\"pages\":\"61 - 74\"},\"PeriodicalIF\":0.5000,\"publicationDate\":\"2021-01-21\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"https://sci-hub-pdf.com/10.1007/s40062-020-00274-0\",\"citationCount\":\"2\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Journal of Homotopy and Related Structures\",\"FirstCategoryId\":\"100\",\"ListUrlMain\":\"https://link.springer.com/article/10.1007/s40062-020-00274-0\",\"RegionNum\":4,\"RegionCategory\":\"数学\",\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"\",\"PubModel\":\"\",\"JCR\":\"\",\"JCRName\":\"\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Journal of Homotopy and Related Structures","FirstCategoryId":"100","ListUrlMain":"https://link.springer.com/article/10.1007/s40062-020-00274-0","RegionNum":4,"RegionCategory":"数学","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"","JCRName":"","Score":null,"Total":0}

引用次数: 2

摘要

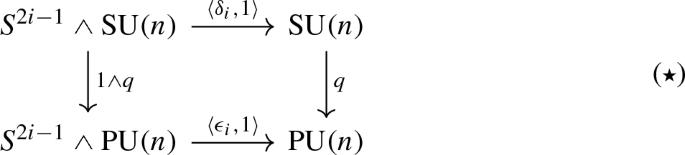
的规范群之间的关系 $\mathrm {SU}(n)$-和 $\mathrm {PU}(n)$-捆起来 $S^{2i}$， with $2\le i\le n$特别是当n是质数时。作为特殊情况，为 $\mathrm {PU}(5)$-捆起来 $S^4$，我们证明了存在一个有理或p局部等价 $\mathcal {G}_{2,k}\simeq _{(p)}\mathcal {G}_{2,l}$ 对于任意' p，当且仅当， $(120,k)=(120,l)$，而对于 $\mathrm {PU}(3)$-捆起来 $S^6$ 这是一个积分等价 $\mathcal {G}_{3,k}\simeq \mathcal {G}_{3,l}$ 当且仅当， $(120,k)=(120,l)$．

本文章由计算机程序翻译，如有差异，请以英文原文为准。

$Homotopy types of gauge groups of $\mathrm {PU}(p)$-bundles over spheres$

查看原文本刊更多论文

Homotopy types of gauge groups of $\mathrm {PU}(p)$-bundles over spheres

We examine the relation between the gauge groups of $\mathrm {SU}(n)$- and $\mathrm {PU}(n)$-bundles over $S^{2i}$, with $2\le i\le n$, particularly when n is a prime. As special cases, for $\mathrm {PU}(5)$-bundles over $S^4$, we show that there is a rational or p-local equivalence $\mathcal {G}_{2,k}\simeq _{(p)}\mathcal {G}_{2,l}$ for any prime p if, and only if, $(120,k)=(120,l)$, while for $\mathrm {PU}(3)$-bundles over $S^6$ there is an integral equivalence $\mathcal {G}_{3,k}\simeq \mathcal {G}_{3,l}$ if, and only if, $(120,k)=(120,l)$.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Journal of Homotopy and Related Structures Mathematics-Geometry and Topology

自引率

0.00%

发文量

期刊介绍： Journal of Homotopy and Related Structures (JHRS) is a fully refereed international journal dealing with homotopy and related structures of mathematical and physical sciences. Journal of Homotopy and Related Structures is intended to publish papers on Homotopy in the broad sense and its related areas like Homological and homotopical algebra, K-theory, topology of manifolds, geometric and categorical structures, homology theories, topological groups and algebras, stable homotopy theory, group actions, algebraic varieties, category theory, cobordism theory, controlled topology, noncommutative geometry, motivic cohomology, differential topology, algebraic geometry.

球上\(\mathrm {PU}(p)\) -束规范群的同伦类型

摘要