两种粘性流体分层流动的线性稳定性

IF 0.3 Q4 MECHANICS

Moscow University Mechanics Bulletin Pub Date : 2022-10-20 DOI:10.3103/S0027133022040021

O. A. Logvinov

{"title":"两种粘性流体分层流动的线性稳定性","authors":"O. A. Logvinov","doi":"10.3103/S0027133022040021","DOIUrl":null,"url":null,"abstract":"<p>Stability to small perturbations of two-layered parabolic flow in a plane channel is analyzed. The dispersion relation between a disturbance wavelength and its growth rate is valid in the whole range of wavenumbers and for moderately large Reynolds numbers. The results coincide with known asymptotic theory conclusions. Besides, a new effect for flows not only with viscosity stratification but also with density stratification is revealed. The agreement with experimental data is acceptable.</p>","PeriodicalId":710,"journal":{"name":"Moscow University Mechanics Bulletin","volume":"77 4","pages":"117 - 126"},"PeriodicalIF":0.3000,"publicationDate":"2022-10-20","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"","citationCount":"0","resultStr":"{\"title\":\"Linear Stability of Stratified Flow of Two Viscous Fluids\",\"authors\":\"O. A. Logvinov\",\"doi\":\"10.3103/S0027133022040021\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"<p>Stability to small perturbations of two-layered parabolic flow in a plane channel is analyzed. The dispersion relation between a disturbance wavelength and its growth rate is valid in the whole range of wavenumbers and for moderately large Reynolds numbers. The results coincide with known asymptotic theory conclusions. Besides, a new effect for flows not only with viscosity stratification but also with density stratification is revealed. The agreement with experimental data is acceptable.</p>\",\"PeriodicalId\":710,\"journal\":{\"name\":\"Moscow University Mechanics Bulletin\",\"volume\":\"77 4\",\"pages\":\"117 - 126\"},\"PeriodicalIF\":0.3000,\"publicationDate\":\"2022-10-20\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"\",\"citationCount\":\"0\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Moscow University Mechanics Bulletin\",\"FirstCategoryId\":\"1085\",\"ListUrlMain\":\"https://link.springer.com/article/10.3103/S0027133022040021\",\"RegionNum\":0,\"RegionCategory\":null,\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"\",\"PubModel\":\"\",\"JCR\":\"Q4\",\"JCRName\":\"MECHANICS\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Moscow University Mechanics Bulletin","FirstCategoryId":"1085","ListUrlMain":"https://link.springer.com/article/10.3103/S0027133022040021","RegionNum":0,"RegionCategory":null,"ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q4","JCRName":"MECHANICS","Score":null,"Total":0}

引用次数: 0

摘要

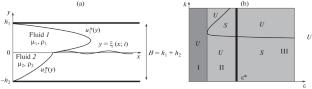
分析了平面通道中两层抛物流的小扰动稳定性。扰动波长与其生长速率之间的色散关系在整个波数范围和中等大的雷诺数范围内都是有效的。所得结果与已知的渐近理论结论一致。此外，还揭示了粘度分层和密度分层对流动的新影响。与实验数据的一致性是可以接受的。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

Linear Stability of Stratified Flow of Two Viscous Fluids

查看原文本刊更多论文

Linear Stability of Stratified Flow of Two Viscous Fluids

Stability to small perturbations of two-layered parabolic flow in a plane channel is analyzed. The dispersion relation between a disturbance wavelength and its growth rate is valid in the whole range of wavenumbers and for moderately large Reynolds numbers. The results coincide with known asymptotic theory conclusions. Besides, a new effect for flows not only with viscosity stratification but also with density stratification is revealed. The agreement with experimental data is acceptable.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Moscow University Mechanics Bulletin MECHANICS-

CiteScore

0.60

自引率

0.00%

发文量

期刊介绍： Moscow University Mechanics Bulletin is the journal of scientific publications, reflecting the most important areas of mechanics at Lomonosov Moscow State University. The journal is dedicated to research in theoretical mechanics, applied mechanics and motion control, hydrodynamics, aeromechanics, gas and wave dynamics, theory of elasticity, theory of elasticity and mechanics of composites.