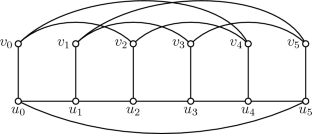
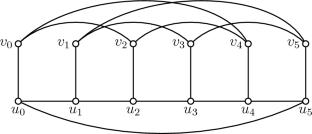
On Distance-Balanced Generalized Petersen Graphs

A connected graph G of diameter \(\textrm{diam}(G) \ge \ell \) is \(\ell \)-distance-balanced if \(|W_{xy}|=|W_{yx}|\) for every \(x,y\in V(G)\) with \(d_{G}(x,y)=\ell \), where \(W_{xy}\) is the set of vertices of G that are closer to x than to y. We prove that the generalized Petersen graph GP(n, k) is \(\textrm{diam}(GP(n,k))\)-distance-balanced provided that n is large enough relative to k. This partially solves a conjecture posed by Miklavič and Šparl (Discrete Appl Math 244:143–154, 2018). We also determine \(\textrm{diam}(GP(n,k))\) when n is large enough relative to k.