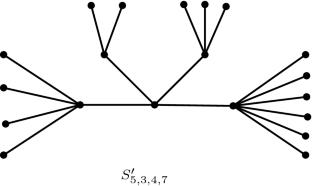
Upper Bounds on the Smallest Positive Eigenvalue of Trees

In this article, we undertake the problem of finding the first four trees on a fixed number of vertices with the maximum smallest positive eigenvalue. Let \({\mathcal {T}}_{n,d}\) denote the class of trees on n vertices with diameter d. First, we obtain the bounds on the smallest positive eigenvalue of trees in \({\mathcal {T}}_{n,d}\) for \(d =2,3,4\) and then upper bounds on the smallest positive eigenvalue of trees are obtained in general class of all trees on n vertices. Finally, the first four trees on n vertices with the maximum, second maximum, third maximum and fourth maximum smallest positive eigenvalue are characterized.