根接近1的AR（1）过程的最小绝对偏差估计

IF 0.8 4区数学 Q3 STATISTICS & PROBABILITY

Annals of the Institute of Statistical Mathematics Pub Date : 2023-01-23 DOI:10.1007/s10463-022-00864-0

Nannan Ma, Hailin Sang, Guangyu Yang

{"title":"根接近1的AR（1）过程的最小绝对偏差估计","authors":"Nannan Ma, Hailin Sang, Guangyu Yang","doi":"10.1007/s10463-022-00864-0","DOIUrl":null,"url":null,"abstract":"<div>We establish the asymptotic theory of least absolute deviation estimators for AR(1) processes with autoregressive parameter satisfying \\(n(\\rho _n-1)\\rightarrow \\gamma\\) for some fixed \\(\\gamma\\) as \\(n\\rightarrow \\infty\\), which is parallel to the results of ordinary least squares estimators developed by Andrews and Guggenberger (Journal of Time Series Analysis, 29, 203–212, 2008) in the case \\(\\gamma = 0\\) or Chan and Wei (Annals of Statistics, 15, 1050–1063, 1987) and Phillips (Biometrika, 74, 535–574, 1987) in the case \\(\\gamma \\ne 0\\). Simulation experiments are conducted to confirm the theoretical results and to demonstrate the robustness of the least absolute deviation estimation.</div>","PeriodicalId":55511,"journal":{"name":"Annals of the Institute of Statistical Mathematics","volume":null,"pages":null},"PeriodicalIF":0.8000,"publicationDate":"2023-01-23","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"","citationCount":"0","resultStr":"{\"title\":\"Least absolute deviation estimation for AR(1) processes with roots close to unity\",\"authors\":\"Nannan Ma, Hailin Sang, Guangyu Yang\",\"doi\":\"10.1007/s10463-022-00864-0\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"<div>We establish the asymptotic theory of least absolute deviation estimators for AR(1) processes with autoregressive parameter satisfying \\\\(n(\\\\rho _n-1)\\\\rightarrow \\\\gamma\\\\) for some fixed \\\\(\\\\gamma\\\\) as \\\\(n\\\\rightarrow \\\\infty\\\\), which is parallel to the results of ordinary least squares estimators developed by Andrews and Guggenberger (Journal of Time Series Analysis, 29, 203–212, 2008) in the case \\\\(\\\\gamma = 0\\\\) or Chan and Wei (Annals of Statistics, 15, 1050–1063, 1987) and Phillips (Biometrika, 74, 535–574, 1987) in the case \\\\(\\\\gamma \\\\ne 0\\\\). Simulation experiments are conducted to confirm the theoretical results and to demonstrate the robustness of the least absolute deviation estimation.</div>\",\"PeriodicalId\":55511,\"journal\":{\"name\":\"Annals of the Institute of Statistical Mathematics\",\"volume\":null,\"pages\":null},\"PeriodicalIF\":0.8000,\"publicationDate\":\"2023-01-23\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"\",\"citationCount\":\"0\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Annals of the Institute of Statistical Mathematics\",\"FirstCategoryId\":\"100\",\"ListUrlMain\":\"https://link.springer.com/article/10.1007/s10463-022-00864-0\",\"RegionNum\":4,\"RegionCategory\":\"数学\",\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"\",\"PubModel\":\"\",\"JCR\":\"Q3\",\"JCRName\":\"STATISTICS & PROBABILITY\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Annals of the Institute of Statistical Mathematics","FirstCategoryId":"100","ListUrlMain":"https://link.springer.com/article/10.1007/s10463-022-00864-0","RegionNum":4,"RegionCategory":"数学","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q3","JCRName":"STATISTICS & PROBABILITY","Score":null,"Total":0}

引用次数: 0

摘要

对于自回归参数满足\(n(\rho _n-1)\rightarrow \gamma\)的AR(1)过程，对于某些固定的\(\gamma\) = \(n\rightarrow \infty\)，我们建立了最小绝对偏差估计量的渐近理论，这与andrew和Guggenberger (Journal of Time Series Analysis, 29,203 - 212,2008)在\(\gamma = 0\)或Chan和Wei (Annals of Statistics, 15,1050 - 1063, 1987)和Phillips (Biometrika, 74,535 - 574)的情况下的普通最小二乘估计量的结果相似。1987)在\(\gamma \ne 0\)的情况下。仿真实验验证了理论结果，并验证了最小绝对偏差估计的鲁棒性。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

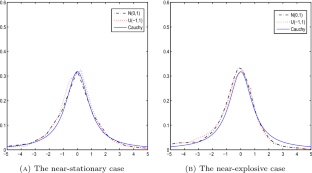
Least absolute deviation estimation for AR(1) processes with roots close to unity

查看原文本刊更多论文

Least absolute deviation estimation for AR(1) processes with roots close to unity

We establish the asymptotic theory of least absolute deviation estimators for AR(1) processes with autoregressive parameter satisfying \(n(\rho _n-1)\rightarrow \gamma\) for some fixed \(\gamma\) as \(n\rightarrow \infty\), which is parallel to the results of ordinary least squares estimators developed by Andrews and Guggenberger (Journal of Time Series Analysis, 29, 203–212, 2008) in the case \(\gamma = 0\) or Chan and Wei (Annals of Statistics, 15, 1050–1063, 1987) and Phillips (Biometrika, 74, 535–574, 1987) in the case \(\gamma \ne 0\). Simulation experiments are conducted to confirm the theoretical results and to demonstrate the robustness of the least absolute deviation estimation.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Annals of the Institute of Statistical Mathematics 数学-统计学与概率论

CiteScore

2.00

自引率

0.00%

发文量

审稿时长

6-12 weeks

期刊介绍： Annals of the Institute of Statistical Mathematics (AISM) aims to provide a forum for open communication among statisticians, and to contribute to the advancement of statistics as a science to enable humans to handle information in order to cope with uncertainties. It publishes high-quality papers that shed new light on the theoretical, computational and/or methodological aspects of statistical science. Emphasis is placed on (a) development of new methodologies motivated by real data, (b) development of unifying theories, and (c) analysis and improvement of existing methodologies and theories.