曲面上的对合

IF 0.7 4区数学 Q2 MATHEMATICS

Journal of Homotopy and Related Structures Pub Date : 2019-05-14 DOI:10.1007/s40062-019-00236-1

Daniel Dugger

{"title":"曲面上的对合","authors":"Daniel Dugger","doi":"10.1007/s40062-019-00236-1","DOIUrl":null,"url":null,"abstract":"<p>We use equivariant surgery to classify all involutions on closed surfaces, up to isomorphism. Work on this problem is classical, dating back to the nineteenth century, with a complete classification finally appearing in the 1990s. In this paper we give a different approach to the classification, using techniques that are more accessible to algebraic topologists as well as a new invariant (which we call the double-Dickson invariant) for distinguishing the “hard” cases.</p>","PeriodicalId":49034,"journal":{"name":"Journal of Homotopy and Related Structures","volume":"14 4","pages":"919 - 992"},"PeriodicalIF":0.7000,"publicationDate":"2019-05-14","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"https://sci-hub-pdf.com/10.1007/s40062-019-00236-1","citationCount":"16","resultStr":"{\"title\":\"Involutions on surfaces\",\"authors\":\"Daniel Dugger\",\"doi\":\"10.1007/s40062-019-00236-1\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"<p>We use equivariant surgery to classify all involutions on closed surfaces, up to isomorphism. Work on this problem is classical, dating back to the nineteenth century, with a complete classification finally appearing in the 1990s. In this paper we give a different approach to the classification, using techniques that are more accessible to algebraic topologists as well as a new invariant (which we call the double-Dickson invariant) for distinguishing the “hard” cases.</p>\",\"PeriodicalId\":49034,\"journal\":{\"name\":\"Journal of Homotopy and Related Structures\",\"volume\":\"14 4\",\"pages\":\"919 - 992\"},\"PeriodicalIF\":0.7000,\"publicationDate\":\"2019-05-14\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"https://sci-hub-pdf.com/10.1007/s40062-019-00236-1\",\"citationCount\":\"16\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Journal of Homotopy and Related Structures\",\"FirstCategoryId\":\"100\",\"ListUrlMain\":\"https://link.springer.com/article/10.1007/s40062-019-00236-1\",\"RegionNum\":4,\"RegionCategory\":\"数学\",\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"\",\"PubModel\":\"\",\"JCR\":\"Q2\",\"JCRName\":\"MATHEMATICS\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Journal of Homotopy and Related Structures","FirstCategoryId":"100","ListUrlMain":"https://link.springer.com/article/10.1007/s40062-019-00236-1","RegionNum":4,"RegionCategory":"数学","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q2","JCRName":"MATHEMATICS","Score":null,"Total":0}

引用次数: 16

摘要

我们用等变手术对闭合表面上的所有对合进行分类，直到同构。关于这个问题的研究是经典的，可以追溯到19世纪，直到20世纪90年代才出现了一个完整的分类。在本文中，我们给出了一种不同的分类方法，使用代数拓扑学家更容易理解的技术以及一个新的不变量(我们称之为double-Dickson不变量)来区分“困难”情况。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

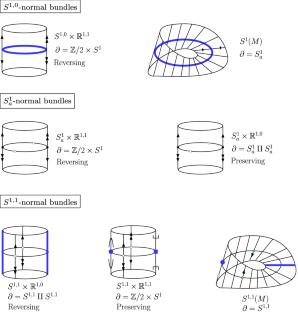
Involutions on surfaces

查看原文本刊更多论文

Involutions on surfaces

We use equivariant surgery to classify all involutions on closed surfaces, up to isomorphism. Work on this problem is classical, dating back to the nineteenth century, with a complete classification finally appearing in the 1990s. In this paper we give a different approach to the classification, using techniques that are more accessible to algebraic topologists as well as a new invariant (which we call the double-Dickson invariant) for distinguishing the “hard” cases.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Journal of Homotopy and Related Structures MATHEMATICS-

CiteScore

1.20

自引率

0.00%

发文量

审稿时长

>12 weeks

期刊介绍： Journal of Homotopy and Related Structures (JHRS) is a fully refereed international journal dealing with homotopy and related structures of mathematical and physical sciences. Journal of Homotopy and Related Structures is intended to publish papers on Homotopy in the broad sense and its related areas like Homological and homotopical algebra, K-theory, topology of manifolds, geometric and categorical structures, homology theories, topological groups and algebras, stable homotopy theory, group actions, algebraic varieties, category theory, cobordism theory, controlled topology, noncommutative geometry, motivic cohomology, differential topology, algebraic geometry.