分支裂纹的数值模拟
IF 0.7
Q4 MECHANICS
引用次数: 0
摘要
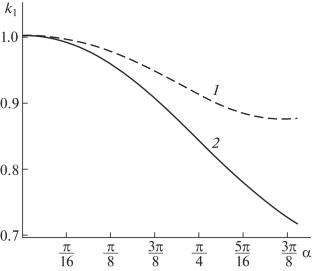
随着体中各种微缺陷的生长,可以产生任意形态的复杂裂纹系统。本文提出了一种复杂分支裂纹的数值模拟技术,使这类系统的分析成为可能。利用本文提出的方法,可以找到应力场、位移场和应力强度因子,并对其进行分析,得出考虑的形态对裂纹稳定性影响的结论。本文还与其他作者在双连杆裂纹问题上的结果进行了比较。本文章由计算机程序翻译,如有差异,请以英文原文为准。
Numerical Modeling of Branched Cracks
With the growth of various microdefects in bodies, complex systems of cracks of arbitrary configuration can be generated. This paper presents a technique for numerical simulation of complex branched cracks, which makes it possible to analyze such systems. Using the method proposed by the authors, it is possible to find the stress and displacement fields as well as the stress intensity factors, the analysis of which leads to the conclusion about the influence of the considered configuration on the crack stability. The paper also contains the comparison with the results of other authors in the problem of a two-link crack.
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊

Moscow University Mechanics Bulletin
MECHANICS-
CiteScore
0.60
自引率
0.00%
发文量
9
期刊介绍:
Moscow University Mechanics Bulletin is the journal of scientific publications, reflecting the most important areas of mechanics at Lomonosov Moscow State University. The journal is dedicated to research in theoretical mechanics, applied mechanics and motion control, hydrodynamics, aeromechanics, gas and wave dynamics, theory of elasticity, theory of elasticity and mechanics of composites.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


