正交和辛随机张量模型的对偶性:一般不变量

IF 1.3 3区物理与天体物理 Q3 PHYSICS, MATHEMATICAL

Letters in Mathematical Physics Pub Date : 2023-07-12 DOI:10.1007/s11005-023-01706-7

Hannes Keppler, Thomas Muller

{"title":"正交和辛随机张量模型的对偶性:一般不变量","authors":"Hannes Keppler, Thomas Muller","doi":"10.1007/s11005-023-01706-7","DOIUrl":null,"url":null,"abstract":"<div>In Gurau and Keppler 2022 (arxiv:2207.01993), a relation between orthogonal and symplectic tensor models with quartic interactions was proven. In this paper, we provide an alternative proof that extends to polynomial interactions of arbitrary order. We consider tensor models of order D with no symmetry under permutation of the indices that transform in the tensor product of D fundamental representations of O(N) and Sp(N). We explicitly show that the models obey the N to \\(-N\\) duality graph by graph in perturbation theory.\n</div>","PeriodicalId":685,"journal":{"name":"Letters in Mathematical Physics","volume":"113 4","pages":""},"PeriodicalIF":1.3000,"publicationDate":"2023-07-12","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"https://link.springer.com/content/pdf/10.1007/s11005-023-01706-7.pdf","citationCount":"1","resultStr":"{\"title\":\"Duality of orthogonal and symplectic random tensor models: general invariants\",\"authors\":\"Hannes Keppler, Thomas Muller\",\"doi\":\"10.1007/s11005-023-01706-7\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"<div>In Gurau and Keppler 2022 (arxiv:2207.01993), a relation between orthogonal and symplectic tensor models with quartic interactions was proven. In this paper, we provide an alternative proof that extends to polynomial interactions of arbitrary order. We consider tensor models of order D with no symmetry under permutation of the indices that transform in the tensor product of D fundamental representations of O(N) and Sp(N). We explicitly show that the models obey the N to \\\\(-N\\\\) duality graph by graph in perturbation theory.\\n</div>\",\"PeriodicalId\":685,\"journal\":{\"name\":\"Letters in Mathematical Physics\",\"volume\":\"113 4\",\"pages\":\"\"},\"PeriodicalIF\":1.3000,\"publicationDate\":\"2023-07-12\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"https://link.springer.com/content/pdf/10.1007/s11005-023-01706-7.pdf\",\"citationCount\":\"1\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Letters in Mathematical Physics\",\"FirstCategoryId\":\"101\",\"ListUrlMain\":\"https://link.springer.com/article/10.1007/s11005-023-01706-7\",\"RegionNum\":3,\"RegionCategory\":\"物理与天体物理\",\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"\",\"PubModel\":\"\",\"JCR\":\"Q3\",\"JCRName\":\"PHYSICS, MATHEMATICAL\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Letters in Mathematical Physics","FirstCategoryId":"101","ListUrlMain":"https://link.springer.com/article/10.1007/s11005-023-01706-7","RegionNum":3,"RegionCategory":"物理与天体物理","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q3","JCRName":"PHYSICS, MATHEMATICAL","Score":null,"Total":0}

引用次数: 1

摘要

在Gurau and Keppler 2022 (arxiv:2207.01993)中，证明了具有四次相互作用的正交张量模型与辛张量模型之间的关系。在本文中，我们提供了一种扩展到任意阶多项式相互作用的替代证明。我们考虑在O(N)和Sp(N)的D种基本表示的张量积中变换的指标的置换下无对称的D阶张量模型。在摄动理论中，我们明确地证明了模型服从N到\(-N\)对偶图。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

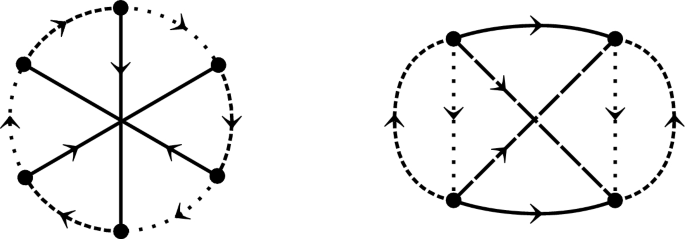
Duality of orthogonal and symplectic random tensor models: general invariants

查看原文本刊更多论文

Duality of orthogonal and symplectic random tensor models: general invariants

In Gurau and Keppler 2022 (arxiv:2207.01993), a relation between orthogonal and symplectic tensor models with quartic interactions was proven. In this paper, we provide an alternative proof that extends to polynomial interactions of arbitrary order. We consider tensor models of order D with no symmetry under permutation of the indices that transform in the tensor product of D fundamental representations of O(N) and Sp(N). We explicitly show that the models obey the N to \(-N\) duality graph by graph in perturbation theory.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Letters in Mathematical Physics 物理-物理：数学物理

CiteScore

2.40

自引率

8.30%

发文量

111

审稿时长

3 months

期刊介绍： The aim of Letters in Mathematical Physics is to attract the community''s attention on important and original developments in the area of mathematical physics and contemporary theoretical physics. The journal publishes letters and longer research articles, occasionally also articles containing topical reviews. We are committed to both fast publication and careful refereeing. In addition, the journal offers important contributions to modern mathematics in fields which have a potential physical application, and important developments in theoretical physics which have potential mathematical impact.