准稳定理想的Pommaret-Seiler解析的元胞结构

IF 0.6 4区工程技术 Q4 COMPUTER SCIENCE, INTERDISCIPLINARY APPLICATIONS

Applicable Algebra in Engineering Communication and Computing Pub Date : 2022-10-13 DOI:10.1007/s00200-022-00584-1

Rodrigo Iglesias, Eduardo Sáenz-de-Cabezón

{"title":"准稳定理想的Pommaret-Seiler解析的元胞结构","authors":"Rodrigo Iglesias, Eduardo Sáenz-de-Cabezón","doi":"10.1007/s00200-022-00584-1","DOIUrl":null,"url":null,"abstract":"<div><p>We prove that the Pommaret-Seiler resolution for quasi-stable ideals is cellular and give a cellular structure for it. This shows that this resolution is a generalization of the well known Eliahou–Kervaire resolution for stable ideals in a deeper sense. We also prove that the Pommaret-Seiler resolution can be reduced to the minimal one via Discrete Morse Theory and provide a constructive algorithm to perform this reduction.</p></div>","PeriodicalId":50742,"journal":{"name":"Applicable Algebra in Engineering Communication and Computing","volume":null,"pages":null},"PeriodicalIF":0.6000,"publicationDate":"2022-10-13","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"","citationCount":"0","resultStr":"{\"title\":\"Cellular structure of the Pommaret-Seiler resolution for quasi-stable ideals\",\"authors\":\"Rodrigo Iglesias, Eduardo Sáenz-de-Cabezón\",\"doi\":\"10.1007/s00200-022-00584-1\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"<div><p>We prove that the Pommaret-Seiler resolution for quasi-stable ideals is cellular and give a cellular structure for it. This shows that this resolution is a generalization of the well known Eliahou–Kervaire resolution for stable ideals in a deeper sense. We also prove that the Pommaret-Seiler resolution can be reduced to the minimal one via Discrete Morse Theory and provide a constructive algorithm to perform this reduction.</p></div>\",\"PeriodicalId\":50742,\"journal\":{\"name\":\"Applicable Algebra in Engineering Communication and Computing\",\"volume\":null,\"pages\":null},\"PeriodicalIF\":0.6000,\"publicationDate\":\"2022-10-13\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"\",\"citationCount\":\"0\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Applicable Algebra in Engineering Communication and Computing\",\"FirstCategoryId\":\"5\",\"ListUrlMain\":\"https://link.springer.com/article/10.1007/s00200-022-00584-1\",\"RegionNum\":4,\"RegionCategory\":\"工程技术\",\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"\",\"PubModel\":\"\",\"JCR\":\"Q4\",\"JCRName\":\"COMPUTER SCIENCE, INTERDISCIPLINARY APPLICATIONS\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Applicable Algebra in Engineering Communication and Computing","FirstCategoryId":"5","ListUrlMain":"https://link.springer.com/article/10.1007/s00200-022-00584-1","RegionNum":4,"RegionCategory":"工程技术","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q4","JCRName":"COMPUTER SCIENCE, INTERDISCIPLINARY APPLICATIONS","Score":null,"Total":0}

引用次数: 0

摘要

我们证明了准稳定理想的 Pommaret-Seiler 解析是蜂窝状的，并给出了它的蜂窝状结构。这表明该解析是众所周知的稳定理想的 Eliahou-Kervaire 解析在更深意义上的泛化。我们还证明了 Pommaret-Seiler 解析可以通过离散莫尔斯理论还原为最小解析，并提供了进行还原的构造算法。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

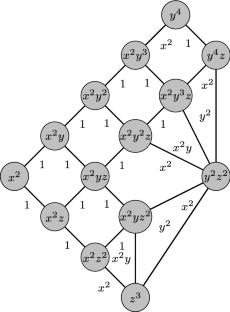
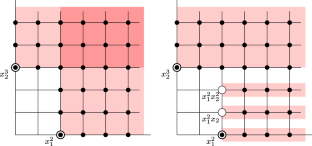
Cellular structure of the Pommaret-Seiler resolution for quasi-stable ideals

查看原文本刊更多论文

Cellular structure of the Pommaret-Seiler resolution for quasi-stable ideals

We prove that the Pommaret-Seiler resolution for quasi-stable ideals is cellular and give a cellular structure for it. This shows that this resolution is a generalization of the well known Eliahou–Kervaire resolution for stable ideals in a deeper sense. We also prove that the Pommaret-Seiler resolution can be reduced to the minimal one via Discrete Morse Theory and provide a constructive algorithm to perform this reduction.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Applicable Algebra in Engineering Communication and Computing 工程技术-计算机：跨学科应用

CiteScore

2.90

自引率

14.30%

发文量

审稿时长

>12 weeks

期刊介绍： Algebra is a common language for many scientific domains. In developing this language mathematicians prove theorems and design methods which demonstrate the applicability of algebra. Using this language scientists in many fields find algebra indispensable to create methods, techniques and tools to solve their specific problems. Applicable Algebra in Engineering, Communication and Computing will publish mathematically rigorous, original research papers reporting on algebraic methods and techniques relevant to all domains concerned with computers, intelligent systems and communications. Its scope includes, but is not limited to, vision, robotics, system design, fault tolerance and dependability of systems, VLSI technology, signal processing, signal theory, coding, error control techniques, cryptography, protocol specification, networks, software engineering, arithmetics, algorithms, complexity, computer algebra, programming languages, logic and functional programming, algebraic specification, term rewriting systems, theorem proving, graphics, modeling, knowledge engineering, expert systems, and artificial intelligence methodology. Purely theoretical papers will not primarily be sought, but papers dealing with problems in such domains as commutative or non-commutative algebra, group theory, field theory, or real algebraic geometry, which are of interest for applications in the above mentioned fields are relevant for this journal. On the practical side, technology and know-how transfer papers from engineering which either stimulate or illustrate research in applicable algebra are within the scope of the journal.