逐点James型常数
IF 0.6
3区 数学
Q3 MATHEMATICS
引用次数: 0
摘要
2008年,高桥引入了James类型的常量。本文讨论了点态James型常数:对于所有x∈x,∈x∈=1,我们证明了在几乎可传递Banach空间中,映射x∈x,∈↦ J(x,x,t)是常数。因此,考虑到Mazur旋转问题,我们证明了对于几乎传递Banach空间,对于某个单位向量x∈x,条件\(J(x,x,t)=\sqrt 2\)意味着x是Hilbert。本文章由计算机程序翻译,如有差异,请以英文原文为准。
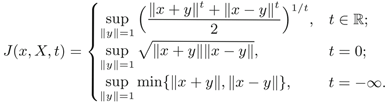
The pointwise James type constant
In 2008, Takahashi introduced the James type constants. We discuss here the pointwise James type constant: for all x ∈ X, ∥x∥ = 1,
We show that in almost transitive Banach spaces, the map x ∈ X, ∥x∥ = 1 ↦ J(x, X, t) is constant. As a consequence and having in mind the Mazur’s rotation problem, we prove that for almost transitive Banach spaces, the condition \(J(x,X,t) = \sqrt 2 \) for some unit vector x ∈ X implies that X is Hilbert.
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊

Analysis Mathematica
MATHEMATICS-
CiteScore
1.00
自引率
14.30%
发文量
54
审稿时长
>12 weeks
期刊介绍:
Traditionally the emphasis of Analysis Mathematica is classical analysis, including real functions (MSC 2010: 26xx), measure and integration (28xx), functions of a complex variable (30xx), special functions (33xx), sequences, series, summability (40xx), approximations and expansions (41xx).
The scope also includes potential theory (31xx), several complex variables and analytic spaces (32xx), harmonic analysis on Euclidean spaces (42xx), abstract harmonic analysis (43xx).
The journal willingly considers papers in difference and functional equations (39xx), functional analysis (46xx), operator theory (47xx), analysis on topological groups and metric spaces, matrix analysis, discrete versions of topics in analysis, convex and geometric analysis and the interplay between geometry and analysis.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


