线性向量自回归模型中一种新的唯一脉冲响应函数

IF 1.8 4区经济学 Q2 BUSINESS, FINANCE

International Review of Finance Pub Date : 2022-10-03 DOI:10.1111/irfi.12396

Yanlin Shi

{"title":"线性向量自回归模型中一种新的唯一脉冲响应函数","authors":"Yanlin Shi","doi":"10.1111/irfi.12396","DOIUrl":null,"url":null,"abstract":"<p>This article proposes a new unique impulse response function (IRF) measure, or MIRF, based on the popular vector autoregressive model to study interdependency of multivariate time series. Same as the orthogonal IRF, the estimator of MIRF has an analytical form with well-established asymptotics, and is invariant to ordering of series. Compared to alternative unique IRF measures, MIRF does not depend on extreme identifications, and the associated forecast error variance measure is explainable. An illustrative empirical example is also provided.</p>","PeriodicalId":46664,"journal":{"name":"International Review of Finance","volume":"23 2","pages":"460-468"},"PeriodicalIF":1.8000,"publicationDate":"2022-10-03","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"https://onlinelibrary.wiley.com/doi/epdf/10.1111/irfi.12396","citationCount":"0","resultStr":"{\"title\":\"A new unique impulse response function in linear vector autoregressive models\",\"authors\":\"Yanlin Shi\",\"doi\":\"10.1111/irfi.12396\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"<p>This article proposes a new unique impulse response function (IRF) measure, or MIRF, based on the popular vector autoregressive model to study interdependency of multivariate time series. Same as the orthogonal IRF, the estimator of MIRF has an analytical form with well-established asymptotics, and is invariant to ordering of series. Compared to alternative unique IRF measures, MIRF does not depend on extreme identifications, and the associated forecast error variance measure is explainable. An illustrative empirical example is also provided.</p>\",\"PeriodicalId\":46664,\"journal\":{\"name\":\"International Review of Finance\",\"volume\":\"23 2\",\"pages\":\"460-468\"},\"PeriodicalIF\":1.8000,\"publicationDate\":\"2022-10-03\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"https://onlinelibrary.wiley.com/doi/epdf/10.1111/irfi.12396\",\"citationCount\":\"0\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"International Review of Finance\",\"FirstCategoryId\":\"96\",\"ListUrlMain\":\"https://onlinelibrary.wiley.com/doi/10.1111/irfi.12396\",\"RegionNum\":4,\"RegionCategory\":\"经济学\",\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"\",\"PubModel\":\"\",\"JCR\":\"Q2\",\"JCRName\":\"BUSINESS, FINANCE\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"International Review of Finance","FirstCategoryId":"96","ListUrlMain":"https://onlinelibrary.wiley.com/doi/10.1111/irfi.12396","RegionNum":4,"RegionCategory":"经济学","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q2","JCRName":"BUSINESS, FINANCE","Score":null,"Total":0}

引用次数: 0

摘要

本文在流行的向量自回归模型的基础上，提出了一种新的独特脉冲响应函数（IRF）测度，即MIRF，来研究多变量时间序列的相关性。与正交IRF一样，MIRF的估计器具有一种具有公认渐近性的分析形式，并且对级数的排序是不变的。与替代的唯一IRF度量相比，MIRF不依赖于极端识别，并且相关的预测误差方差度量是可解释的。还提供了一个说明性的经验示例。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

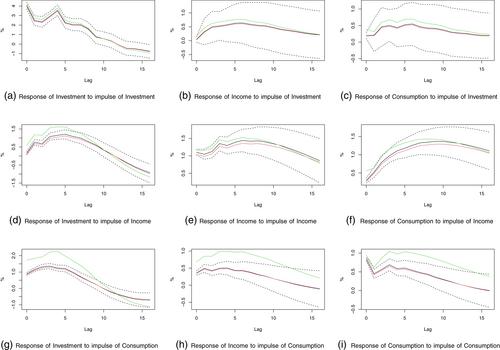
A new unique impulse response function in linear vector autoregressive models

查看原文本刊更多论文

A new unique impulse response function in linear vector autoregressive models

This article proposes a new unique impulse response function (IRF) measure, or MIRF, based on the popular vector autoregressive model to study interdependency of multivariate time series. Same as the orthogonal IRF, the estimator of MIRF has an analytical form with well-established asymptotics, and is invariant to ordering of series. Compared to alternative unique IRF measures, MIRF does not depend on extreme identifications, and the associated forecast error variance measure is explainable. An illustrative empirical example is also provided.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

International Review of Finance BUSINESS, FINANCE-

CiteScore

3.30

自引率

5.90%

发文量

期刊介绍： The International Review of Finance (IRF) publishes high-quality research on all aspects of financial economics, including traditional areas such as asset pricing, corporate finance, market microstructure, financial intermediation and regulation, financial econometrics, financial engineering and risk management, as well as new areas such as markets and institutions of emerging market economies, especially those in the Asia-Pacific region. In addition, the Letters Section in IRF is a premium outlet of letter-length research in all fields of finance. The length of the articles in the Letters Section is limited to a maximum of eight journal pages.