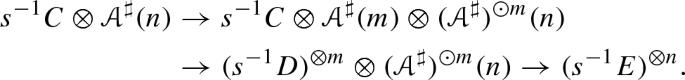
Twisting structures and morphisms up to strong homotopy

We define twisted composition products of symmetric sequences via classifying morphisms rather than twisting cochains. Our approach allows us to establish an adjunction that simultaneously generalizes a classic one for algebras and coalgebras, and the bar-cobar adjunction for quadratic operads. The comonad associated to this adjunction turns out to be, in several cases, a standard Koszul construction. The associated Kleisli categories are the “strong homotopy” morphism categories. In an appendix, we study the co-ring associated to the canonical morphism of cooperads , which is exactly the two-sided Koszul resolution of the associative operad , also known as the Alexander-Whitney co-ring.