霍奇金-赫胥黎模型的修正与神经生理学“全有或全无”法则的数学解释
IF 0.3
Q4 MECHANICS
引用次数: 0
摘要
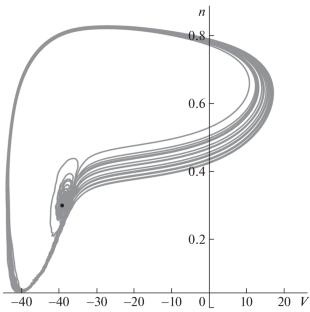
本文给出了随机噪声存在下输入初级神经元的简化修正Hodgkin-Huxley模型的仿真结果。考虑了从稳定焦点的点吸引域到周期吸引域的过渡和到点吸引域的逆过渡。一些例子,其中这种转变可能反复交替,已经获得了主要的神经生理学“全有或无”定律的数学解释。本文章由计算机程序翻译,如有差异,请以英文原文为准。
A Modification of the Hodgkin–Huxley Model and a Mathematical Interpretation of the Principal Neurophysiological ‘‘All-or-None’’ Law
The paper presents the results of simulation with the simplified modified Hodgkin–Huxley model of an afferent primary neuron in the presence of stochastic noise. The transition from the attraction domain of a point attractor like a stable focus to the attraction domain of a periodic attractor and the inverse transition to the attraction domain of the point attractor are considered. Some examples, in which such transitions may be repeatedly alternated, have been obtained as a mathematical interpretation of the principal neurophysiological ‘‘all-or-none’’ law.
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊

Moscow University Mechanics Bulletin
MECHANICS-
CiteScore
0.60
自引率
0.00%
发文量
9
期刊介绍:
Moscow University Mechanics Bulletin is the journal of scientific publications, reflecting the most important areas of mechanics at Lomonosov Moscow State University. The journal is dedicated to research in theoretical mechanics, applied mechanics and motion control, hydrodynamics, aeromechanics, gas and wave dynamics, theory of elasticity, theory of elasticity and mechanics of composites.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


