摄动振荡系统的可达性集与鲁棒稳定性

IF 0.3 Q4 MECHANICS

Moscow University Mechanics Bulletin Pub Date : 2021-07-06 DOI:10.3103/S0027133021010027

V. V. Aleksandrov, D. I. Bugrov, V. N. Zhermolenko, I. S. Konovalenko

{"title":"摄动振荡系统的可达性集与鲁棒稳定性","authors":"V. V. Aleksandrov, D. I. Bugrov, V. N. Zhermolenko, I. S. Konovalenko","doi":"10.3103/S0027133021010027","DOIUrl":null,"url":null,"abstract":"<p>The second-order oscillatory system with constant coefficients in the presence of a time-varying bounded external perturbation is considered. Extreme points of the limit cycle, the boundary of the attainability set, are determined. The limit cycle is used to obtain the quality estimates of the system robust stability against the time-varying perturbation.</p>","PeriodicalId":710,"journal":{"name":"Moscow University Mechanics Bulletin","volume":"76 1","pages":"30 - 34"},"PeriodicalIF":0.3000,"publicationDate":"2021-07-06","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"","citationCount":"3","resultStr":"{\"title\":\"Attainability Set and Robust Stability of Perturbed Oscillatory Systems\",\"authors\":\"V. V. Aleksandrov, D. I. Bugrov, V. N. Zhermolenko, I. S. Konovalenko\",\"doi\":\"10.3103/S0027133021010027\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"<p>The second-order oscillatory system with constant coefficients in the presence of a time-varying bounded external perturbation is considered. Extreme points of the limit cycle, the boundary of the attainability set, are determined. The limit cycle is used to obtain the quality estimates of the system robust stability against the time-varying perturbation.</p>\",\"PeriodicalId\":710,\"journal\":{\"name\":\"Moscow University Mechanics Bulletin\",\"volume\":\"76 1\",\"pages\":\"30 - 34\"},\"PeriodicalIF\":0.3000,\"publicationDate\":\"2021-07-06\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"\",\"citationCount\":\"3\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Moscow University Mechanics Bulletin\",\"FirstCategoryId\":\"1085\",\"ListUrlMain\":\"https://link.springer.com/article/10.3103/S0027133021010027\",\"RegionNum\":0,\"RegionCategory\":null,\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"\",\"PubModel\":\"\",\"JCR\":\"Q4\",\"JCRName\":\"MECHANICS\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Moscow University Mechanics Bulletin","FirstCategoryId":"1085","ListUrlMain":"https://link.springer.com/article/10.3103/S0027133021010027","RegionNum":0,"RegionCategory":null,"ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q4","JCRName":"MECHANICS","Score":null,"Total":0}

引用次数: 3

摘要

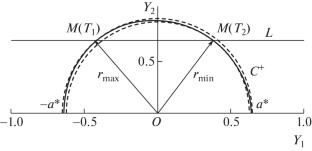
研究了具有时变有界外部扰动的常系数二阶振荡系统。确定了极限环的极值点，即可达集的边界。利用极限环得到系统对时变扰动鲁棒稳定性的质量估计。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

Attainability Set and Robust Stability of Perturbed Oscillatory Systems

查看原文本刊更多论文

Attainability Set and Robust Stability of Perturbed Oscillatory Systems

The second-order oscillatory system with constant coefficients in the presence of a time-varying bounded external perturbation is considered. Extreme points of the limit cycle, the boundary of the attainability set, are determined. The limit cycle is used to obtain the quality estimates of the system robust stability against the time-varying perturbation.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Moscow University Mechanics Bulletin MECHANICS-

CiteScore

0.60

自引率

0.00%

发文量

期刊介绍： Moscow University Mechanics Bulletin is the journal of scientific publications, reflecting the most important areas of mechanics at Lomonosov Moscow State University. The journal is dedicated to research in theoretical mechanics, applied mechanics and motion control, hydrodynamics, aeromechanics, gas and wave dynamics, theory of elasticity, theory of elasticity and mechanics of composites.