简单剪切下Gordon-Schowalter目标导数族的拉格朗日表示
IF 0.3
Q4 MECHANICS
引用次数: 0
摘要
本文章由计算机程序翻译,如有差异,请以英文原文为准。
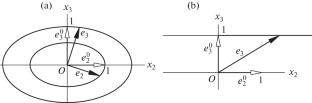
Lagrangian Representation of the Family of Gordon–Schowalter Objective Derivatives at Simple Shear
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊

Moscow University Mechanics Bulletin
MECHANICS-
CiteScore
0.60
自引率
0.00%
发文量
9
期刊介绍:
Moscow University Mechanics Bulletin is the journal of scientific publications, reflecting the most important areas of mechanics at Lomonosov Moscow State University. The journal is dedicated to research in theoretical mechanics, applied mechanics and motion control, hydrodynamics, aeromechanics, gas and wave dynamics, theory of elasticity, theory of elasticity and mechanics of composites.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


