变分的积分分解

IF 0.6 3区数学 Q3 MATHEMATICS

Annals of Global Analysis and Geometry Pub Date : 2023-06-21 DOI:10.1007/s10455-023-09908-x

Hsin-Chuang Chou

{"title":"变分的积分分解","authors":"Hsin-Chuang Chou","doi":"10.1007/s10455-023-09908-x","DOIUrl":null,"url":null,"abstract":"<div><p>This paper introduces a notion of decompositions of integral varifolds into countably many integral varifolds, and the existence of such decomposition of integral varifolds whose first variation is representable by integration is established. However, the decompositions may fail to be unique. Furthermore, this result can be generalized by replacing the class of integral varifolds with some classes of rectifiable varifolds whose density is uniformly bounded from below; for these classes, we also prove a general version of the compactness theorem for integral varifolds.</p></div>","PeriodicalId":8268,"journal":{"name":"Annals of Global Analysis and Geometry","volume":"64 1","pages":""},"PeriodicalIF":0.6000,"publicationDate":"2023-06-21","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"","citationCount":"2","resultStr":"{\"title\":\"Integral decompositions of varifolds\",\"authors\":\"Hsin-Chuang Chou\",\"doi\":\"10.1007/s10455-023-09908-x\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"<div><p>This paper introduces a notion of decompositions of integral varifolds into countably many integral varifolds, and the existence of such decomposition of integral varifolds whose first variation is representable by integration is established. However, the decompositions may fail to be unique. Furthermore, this result can be generalized by replacing the class of integral varifolds with some classes of rectifiable varifolds whose density is uniformly bounded from below; for these classes, we also prove a general version of the compactness theorem for integral varifolds.</p></div>\",\"PeriodicalId\":8268,\"journal\":{\"name\":\"Annals of Global Analysis and Geometry\",\"volume\":\"64 1\",\"pages\":\"\"},\"PeriodicalIF\":0.6000,\"publicationDate\":\"2023-06-21\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"\",\"citationCount\":\"2\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Annals of Global Analysis and Geometry\",\"FirstCategoryId\":\"100\",\"ListUrlMain\":\"https://link.springer.com/article/10.1007/s10455-023-09908-x\",\"RegionNum\":3,\"RegionCategory\":\"数学\",\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"\",\"PubModel\":\"\",\"JCR\":\"Q3\",\"JCRName\":\"MATHEMATICS\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Annals of Global Analysis and Geometry","FirstCategoryId":"100","ListUrlMain":"https://link.springer.com/article/10.1007/s10455-023-09908-x","RegionNum":3,"RegionCategory":"数学","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q3","JCRName":"MATHEMATICS","Score":null,"Total":0}

引用次数: 2

摘要

本文引入了将积分变分分解为可数多个积分变分的概念，并证明了第一个变分可以用积分表示的积分变分这种分解的存在性。然而，分解可能不是唯一的。此外，这一结果可以通过用一些密度从下一致有界的可直变分替换积分变分类来推广；对于这些类，我们还证明了积分变分紧致性定理的一般形式。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

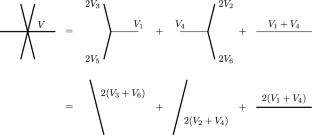
Integral decompositions of varifolds

查看原文本刊更多论文

Integral decompositions of varifolds

This paper introduces a notion of decompositions of integral varifolds into countably many integral varifolds, and the existence of such decomposition of integral varifolds whose first variation is representable by integration is established. However, the decompositions may fail to be unique. Furthermore, this result can be generalized by replacing the class of integral varifolds with some classes of rectifiable varifolds whose density is uniformly bounded from below; for these classes, we also prove a general version of the compactness theorem for integral varifolds.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Annals of Global Analysis and Geometry 数学-数学

CiteScore

1.20

自引率

0.00%

发文量

审稿时长

6-12 weeks

期刊介绍： This journal examines global problems of geometry and analysis as well as the interactions between these fields and their application to problems of theoretical physics. It contributes to an enlargement of the international exchange of research results in the field. The areas covered in Annals of Global Analysis and Geometry include: global analysis, differential geometry, complex manifolds and related results from complex analysis and algebraic geometry, Lie groups, Lie transformation groups and harmonic analysis, variational calculus, applications of differential geometry and global analysis to problems of theoretical physics.