第二和第三共振区边界附近的Mathieu方程

IF 0.3 Q4 MECHANICS

Moscow University Mechanics Bulletin Pub Date : 2022-03-04 DOI:10.3103/S0027133021060030

V. M. Budanov, L. F. Davudova

{"title":"第二和第三共振区边界附近的Mathieu方程","authors":"V. M. Budanov, L. F. Davudova","doi":"10.3103/S0027133021060030","DOIUrl":null,"url":null,"abstract":"<p>A second-order differential equation with periodic coefficients is considered. The reduction of this equation to a first-order nonlinear equation is shown. The fourth approximation of the second resonance zone and the third approximation of the third resonance zone are constructed for the Mathieu equation describing the behavior of solutions near the boundaries of these zones.</p>","PeriodicalId":710,"journal":{"name":"Moscow University Mechanics Bulletin","volume":"76 6","pages":"147 - 155"},"PeriodicalIF":0.3000,"publicationDate":"2022-03-04","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"","citationCount":"0","resultStr":"{\"title\":\"The Mathieu Equation near the Boundaries of the Second and Third Resonance Zones\",\"authors\":\"V. M. Budanov, L. F. Davudova\",\"doi\":\"10.3103/S0027133021060030\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"<p>A second-order differential equation with periodic coefficients is considered. The reduction of this equation to a first-order nonlinear equation is shown. The fourth approximation of the second resonance zone and the third approximation of the third resonance zone are constructed for the Mathieu equation describing the behavior of solutions near the boundaries of these zones.</p>\",\"PeriodicalId\":710,\"journal\":{\"name\":\"Moscow University Mechanics Bulletin\",\"volume\":\"76 6\",\"pages\":\"147 - 155\"},\"PeriodicalIF\":0.3000,\"publicationDate\":\"2022-03-04\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"\",\"citationCount\":\"0\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Moscow University Mechanics Bulletin\",\"FirstCategoryId\":\"1085\",\"ListUrlMain\":\"https://link.springer.com/article/10.3103/S0027133021060030\",\"RegionNum\":0,\"RegionCategory\":null,\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"\",\"PubModel\":\"\",\"JCR\":\"Q4\",\"JCRName\":\"MECHANICS\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Moscow University Mechanics Bulletin","FirstCategoryId":"1085","ListUrlMain":"https://link.springer.com/article/10.3103/S0027133021060030","RegionNum":0,"RegionCategory":null,"ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q4","JCRName":"MECHANICS","Score":null,"Total":0}

引用次数: 0

摘要

研究了一类具有周期系数的二阶微分方程。给出了将该方程化为一阶非线性方程的方法。建立了第二共振带的第四近似和第三共振带的第三近似，给出了描述这些区域边界附近解的行为的Mathieu方程。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

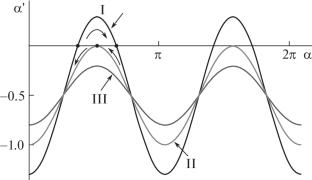
The Mathieu Equation near the Boundaries of the Second and Third Resonance Zones

查看原文本刊更多论文

The Mathieu Equation near the Boundaries of the Second and Third Resonance Zones

A second-order differential equation with periodic coefficients is considered. The reduction of this equation to a first-order nonlinear equation is shown. The fourth approximation of the second resonance zone and the third approximation of the third resonance zone are constructed for the Mathieu equation describing the behavior of solutions near the boundaries of these zones.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Moscow University Mechanics Bulletin MECHANICS-

CiteScore

0.60

自引率

0.00%

发文量

期刊介绍： Moscow University Mechanics Bulletin is the journal of scientific publications, reflecting the most important areas of mechanics at Lomonosov Moscow State University. The journal is dedicated to research in theoretical mechanics, applied mechanics and motion control, hydrodynamics, aeromechanics, gas and wave dynamics, theory of elasticity, theory of elasticity and mechanics of composites.