混合分次模\（infty）-范畴上的一个t-结构

IF 0.5 4区数学

Journal of Homotopy and Related Structures Pub Date : 2023-04-27 DOI:10.1007/s40062-023-00324-3

Emanuele Pavia

{"title":"混合分次模\\（infty）-范畴上的一个t-结构","authors":"Emanuele Pavia","doi":"10.1007/s40062-023-00324-3","DOIUrl":null,"url":null,"abstract":"<div>In this work, we shall study in a purely model-independent fashion the \$\\infty \$-category of mixed graded modules over a ring of characteristic 0, as defined by D. Calaque, T. Pantev, M. Vaquié, B. Toën and G. Vezzosi. First, we collect some basic results about its main formal properties, clarifying foundational questions in a systematic manner, to serve as a reference for future work. Finally, we shall endow such \$\\infty \$-category with a both left and right complete accessible t-structure, showing how this identifies the \$\\infty \$-category of mixed graded modules with the left completion of the Beilinson t-structure on the \$\\infty \$-category of filtered modules.</div>","PeriodicalId":636,"journal":{"name":"Journal of Homotopy and Related Structures","volume":"18 2-3","pages":"177 - 218"},"PeriodicalIF":0.5000,"publicationDate":"2023-04-27","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"https://link.springer.com/content/pdf/10.1007/s40062-023-00324-3.pdf","citationCount":"1","resultStr":"{\"title\":\"A t-structure on the \\\$\\\\infty \\\$-category of mixed graded modules\",\"authors\":\"Emanuele Pavia\",\"doi\":\"10.1007/s40062-023-00324-3\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"<div>In this work, we shall study in a purely model-independent fashion the \\\$\\\\infty \\\$-category of mixed graded modules over a ring of characteristic 0, as defined by D. Calaque, T. Pantev, M. Vaquié, B. Toën and G. Vezzosi. First, we collect some basic results about its main formal properties, clarifying foundational questions in a systematic manner, to serve as a reference for future work. Finally, we shall endow such \\\$\\\\infty \\\$-category with a both left and right complete accessible t-structure, showing how this identifies the \\\$\\\\infty \\\$-category of mixed graded modules with the left completion of the Beilinson t-structure on the \\\$\\\\infty \\\$-category of filtered modules.</div>\",\"PeriodicalId\":636,\"journal\":{\"name\":\"Journal of Homotopy and Related Structures\",\"volume\":\"18 2-3\",\"pages\":\"177 - 218\"},\"PeriodicalIF\":0.5000,\"publicationDate\":\"2023-04-27\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"https://link.springer.com/content/pdf/10.1007/s40062-023-00324-3.pdf\",\"citationCount\":\"1\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Journal of Homotopy and Related Structures\",\"FirstCategoryId\":\"100\",\"ListUrlMain\":\"https://link.springer.com/article/10.1007/s40062-023-00324-3\",\"RegionNum\":4,\"RegionCategory\":\"数学\",\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"\",\"PubModel\":\"\",\"JCR\":\"\",\"JCRName\":\"\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Journal of Homotopy and Related Structures","FirstCategoryId":"100","ListUrlMain":"https://link.springer.com/article/10.1007/s40062-023-00324-3","RegionNum":4,"RegionCategory":"数学","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"","JCRName":"","Score":null,"Total":0}

引用次数: 1

摘要

在这项工作中，我们将以一种纯粹的模型无关的方式研究特征为0的环上的混合分级模的类别，如D.Calaque、T.Pantev、M.Vaquié、B.Toën和G.Vezzosi所定义的。首先，我们收集了一些关于其主要形式性质的基本结果，系统地阐明了一些基本问题，以供今后的工作参考。最后，我们将赋予这类\（\infty\）-范畴一个左和右完全可访问的t-结构，表明这是如何识别混合分级模的\（\infty\）类别与过滤模的\。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

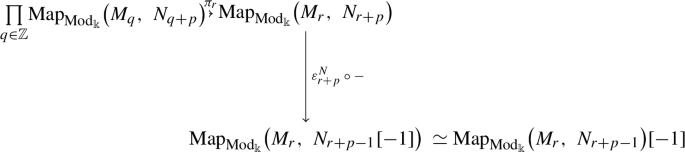
$A t-structure on the $\infty $-category of mixed graded modules$

查看原文本刊更多论文

A t-structure on the $\infty $-category of mixed graded modules

In this work, we shall study in a purely model-independent fashion the $\infty $-category of mixed graded modules over a ring of characteristic 0, as defined by D. Calaque, T. Pantev, M. Vaquié, B. Toën and G. Vezzosi. First, we collect some basic results about its main formal properties, clarifying foundational questions in a systematic manner, to serve as a reference for future work. Finally, we shall endow such $\infty $-category with a both left and right complete accessible t-structure, showing how this identifies the $\infty $-category of mixed graded modules with the left completion of the Beilinson t-structure on the $\infty $-category of filtered modules.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Journal of Homotopy and Related Structures Mathematics-Geometry and Topology

自引率

0.00%

发文量

期刊介绍： Journal of Homotopy and Related Structures (JHRS) is a fully refereed international journal dealing with homotopy and related structures of mathematical and physical sciences. Journal of Homotopy and Related Structures is intended to publish papers on Homotopy in the broad sense and its related areas like Homological and homotopical algebra, K-theory, topology of manifolds, geometric and categorical structures, homology theories, topological groups and algebras, stable homotopy theory, group actions, algebraic varieties, category theory, cobordism theory, controlled topology, noncommutative geometry, motivic cohomology, differential topology, algebraic geometry.