具有非线性发病率的 SEIS 流行病模型的阈值动态。

IF 0.8 Q3 MATHEMATICS, APPLIED

Differential Equations and Dynamical Systems Pub Date : 2021-09-15 DOI:10.1007/s12591-021-00581-9

Mouhcine Naim, Fouad Lahmidi, Abdelwahed Namir

{"title":"具有非线性发病率的 SEIS 流行病模型的阈值动态。","authors":"Mouhcine Naim, Fouad Lahmidi, Abdelwahed Namir","doi":"10.1007/s12591-021-00581-9","DOIUrl":null,"url":null,"abstract":"In this paper, we consider an SEIS epidemic model with infectious force in latent and infected period, which incorporates by nonlinear incidence rates. The local stability of the equilibria is discussed. By means of Lyapunov functionals and LaSalle's invariance principle, we proved the global asymptotic stability of the disease-free equilibrium and the endemic equilibrium. An application is given and numerical simulation results based on real data of COVID-19 in Morocco are performed to justify theoretical findings.","PeriodicalId":45352,"journal":{"name":"Differential Equations and Dynamical Systems","volume":" ","pages":"1-14"},"PeriodicalIF":0.8000,"publicationDate":"2021-09-15","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"https://www.ncbi.nlm.nih.gov/pmc/articles/PMC8441045/pdf/","citationCount":"0","resultStr":"{\"title\":\"<ArticleTitle xmlns:ns0=\\\"http://www.w3.org/1998/Math/MathML\\\">Threshold Dynamics of an <ns0:math><ns0:mi>SEIS</ns0:mi></ns0:math> Epidemic Model with Nonlinear Incidence Rates.\",\"authors\":\"Mouhcine Naim, Fouad Lahmidi, Abdelwahed Namir\",\"doi\":\"10.1007/s12591-021-00581-9\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"In this paper, we consider an SEIS epidemic model with infectious force in latent and infected period, which incorporates by nonlinear incidence rates. The local stability of the equilibria is discussed. By means of Lyapunov functionals and LaSalle's invariance principle, we proved the global asymptotic stability of the disease-free equilibrium and the endemic equilibrium. An application is given and numerical simulation results based on real data of COVID-19 in Morocco are performed to justify theoretical findings.\",\"PeriodicalId\":45352,\"journal\":{\"name\":\"Differential Equations and Dynamical Systems\",\"volume\":\" \",\"pages\":\"1-14\"},\"PeriodicalIF\":0.8000,\"publicationDate\":\"2021-09-15\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"https://www.ncbi.nlm.nih.gov/pmc/articles/PMC8441045/pdf/\",\"citationCount\":\"0\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Differential Equations and Dynamical Systems\",\"FirstCategoryId\":\"1085\",\"ListUrlMain\":\"https://doi.org/10.1007/s12591-021-00581-9\",\"RegionNum\":0,\"RegionCategory\":null,\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"\",\"PubModel\":\"\",\"JCR\":\"Q3\",\"JCRName\":\"MATHEMATICS, APPLIED\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Differential Equations and Dynamical Systems","FirstCategoryId":"1085","ListUrlMain":"https://doi.org/10.1007/s12591-021-00581-9","RegionNum":0,"RegionCategory":null,"ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q3","JCRName":"MATHEMATICS, APPLIED","Score":null,"Total":0}

引用次数: 0

摘要

在本文中，我们考虑了一个 SEIS 流行病模型，该模型在潜伏期和感染期都有感染力，并包含非线性发病率。本文讨论了均衡的局部稳定性。通过莱普诺夫函数和拉萨尔不变性原理，我们证明了无病均衡和流行均衡的全局渐进稳定性。我们给出了一个应用，并根据摩洛哥 COVID-19 的真实数据进行了数值模拟，以证明理论结论的正确性。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

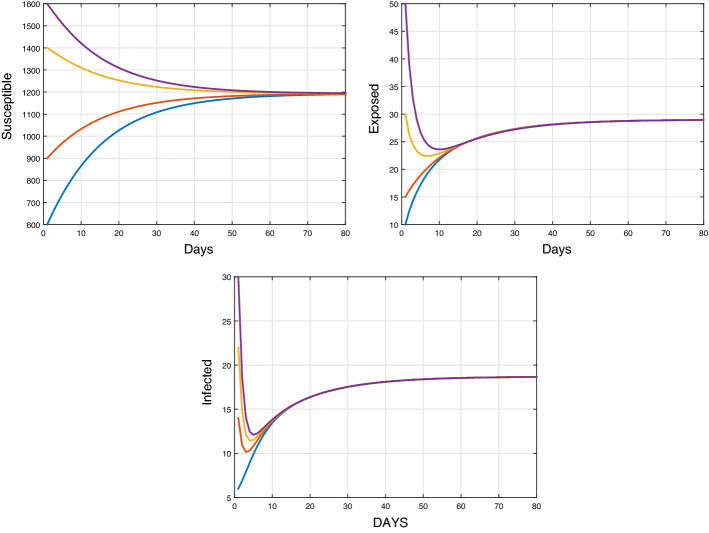
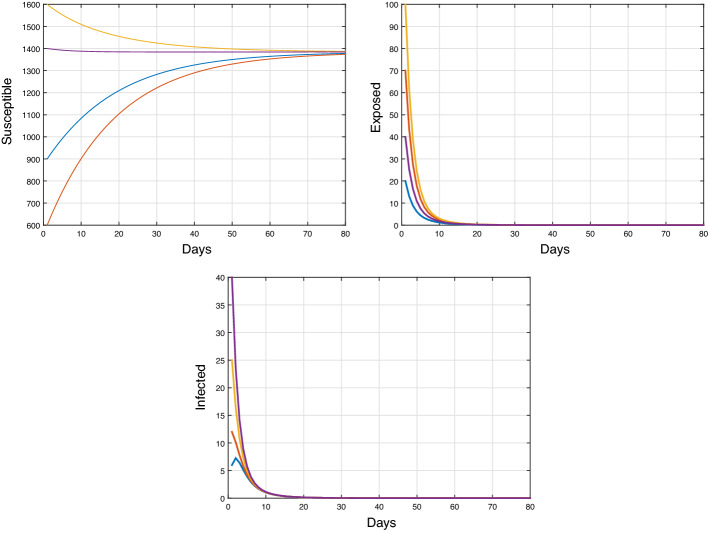
<ArticleTitle xmlns:ns0="http://www.w3.org/1998/Math/MathML">Threshold Dynamics of an <ns0:math><ns0:mi>SEIS</ns0:mi></ns0:math> Epidemic Model with Nonlinear Incidence Rates.

查看原文本刊更多论文

Threshold Dynamics of an SEIS Epidemic Model with Nonlinear Incidence Rates.

In this paper, we consider an SEIS epidemic model with infectious force in latent and infected period, which incorporates by nonlinear incidence rates. The local stability of the equilibria is discussed. By means of Lyapunov functionals and LaSalle's invariance principle, we proved the global asymptotic stability of the disease-free equilibrium and the endemic equilibrium. An application is given and numerical simulation results based on real data of COVID-19 in Morocco are performed to justify theoretical findings.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Differential Equations and Dynamical Systems MATHEMATICS, APPLIED-

CiteScore

3.00

自引率

0.00%

发文量

期刊介绍： Aims and Scope Differential Equations and Dynamical Systems is a multidisciplinary journal whose aim is to publish high quality original research papers in Ordinary and Partial Differential Equations, Integral and Integro-Differential Equations, Calculus of Variations, Bifurcation Theory and Dynamical Systems Theory. Articles devoted to the application of methods and techniques from the above fields of Analysis to Neural Networks, Control Theory; Physical, Biological, Medical, Social and Engineering Sciences are also welcome.In particular, for studies related to modelling aspects in all the above areas, it is essential that the mathematical results be interpreted and translated to the application domains by substantiating the usefulness of the research in solving problems in those realms. Papers dealing with computational and numerical aspects will not be considered for publication unless supported by strong theoretical results and analyses. MissionThe mission of the journal envisages to serve scientists through prompt publication of significant advances in the branches of science and technology beforehand outlined and to provide a forum for the discussion of new scientific developments.