用于时间分数非线性薛定谔方程的五次非多项式样条曲线

IF 4.1 3区数学 Q1 Mathematics

Advances in Difference Equations Pub Date : 2020-01-01 Epub Date: 2020-10-16 DOI:10.1186/s13662-020-03021-0

Qinxu Ding, Patricia J Y Wong

{"title":"用于时间分数非线性薛定谔方程的五次非多项式样条曲线","authors":"Qinxu Ding, Patricia J Y Wong","doi":"10.1186/s13662-020-03021-0","DOIUrl":null,"url":null,"abstract":"In this paper, we shall solve a time-fractional nonlinear Schrödinger equation by using the quintic non-polynomial spline and the L1 formula. The unconditional stability, unique solvability and convergence of our numerical scheme are proved by the Fourier method. It is shown that our method is sixth order accurate in the spatial dimension and <math><mo>(</mo> <mn>2</mn> <mo>-</mo> <mi>γ</mi> <mo>)</mo></math> th order accurate in the temporal dimension, where γ is the fractional order. The efficiency of the proposed numerical scheme is further illustrated by numerical experiments, meanwhile the simulation results indicate better performance over previous work in the literature.","PeriodicalId":53311,"journal":{"name":"Advances in Difference Equations","volume":"2020 1","pages":"577"},"PeriodicalIF":4.1000,"publicationDate":"2020-01-01","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"https://www.ncbi.nlm.nih.gov/pmc/articles/PMC7565234/pdf/","citationCount":"0","resultStr":"{\"title\":\"Quintic non-polynomial spline for time-fractional nonlinear Schrödinger equation.\",\"authors\":\"Qinxu Ding, Patricia J Y Wong\",\"doi\":\"10.1186/s13662-020-03021-0\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"In this paper, we shall solve a time-fractional nonlinear Schrödinger equation by using the quintic non-polynomial spline and the L1 formula. The unconditional stability, unique solvability and convergence of our numerical scheme are proved by the Fourier method. It is shown that our method is sixth order accurate in the spatial dimension and <math><mo>(</mo> <mn>2</mn> <mo>-</mo> <mi>γ</mi> <mo>)</mo></math> th order accurate in the temporal dimension, where γ is the fractional order. The efficiency of the proposed numerical scheme is further illustrated by numerical experiments, meanwhile the simulation results indicate better performance over previous work in the literature.\",\"PeriodicalId\":53311,\"journal\":{\"name\":\"Advances in Difference Equations\",\"volume\":\"2020 1\",\"pages\":\"577\"},\"PeriodicalIF\":4.1000,\"publicationDate\":\"2020-01-01\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"https://www.ncbi.nlm.nih.gov/pmc/articles/PMC7565234/pdf/\",\"citationCount\":\"0\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Advances in Difference Equations\",\"FirstCategoryId\":\"100\",\"ListUrlMain\":\"https://doi.org/10.1186/s13662-020-03021-0\",\"RegionNum\":3,\"RegionCategory\":\"数学\",\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"2020/10/16 0:00:00\",\"PubModel\":\"Epub\",\"JCR\":\"Q1\",\"JCRName\":\"Mathematics\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Advances in Difference Equations","FirstCategoryId":"100","ListUrlMain":"https://doi.org/10.1186/s13662-020-03021-0","RegionNum":3,"RegionCategory":"数学","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"2020/10/16 0:00:00","PubModel":"Epub","JCR":"Q1","JCRName":"Mathematics","Score":null,"Total":0}

引用次数: 0

摘要

本文将利用五次非多项式样条线和 L1 公式求解一个时分数非线性薛定谔方程。我们用傅里叶方法证明了数值方案的无条件稳定性、唯一可解性和收敛性。结果表明，我们的方法在空间维度上具有六阶精度，在时间维度上具有 ( 2 - γ ) 三阶精度，其中 γ 是分数阶。数值实验进一步说明了所提数值方案的效率，同时仿真结果表明其性能优于之前的文献研究。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

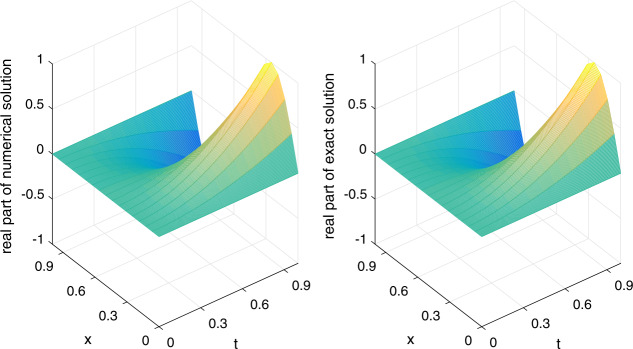
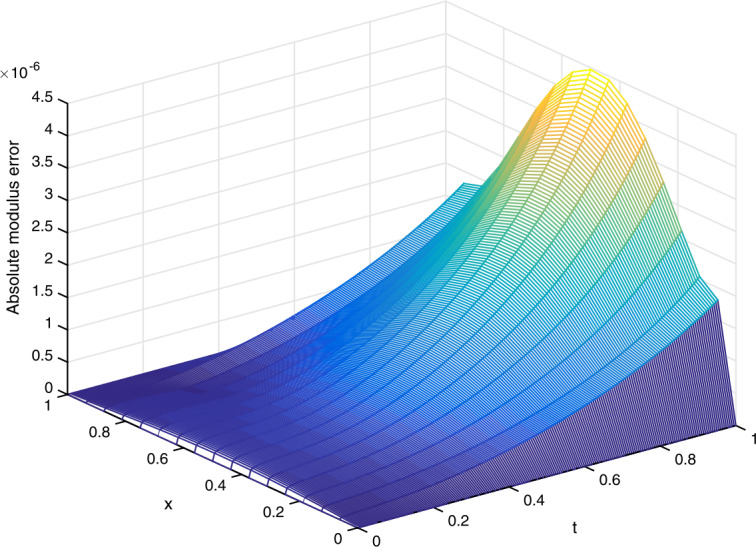
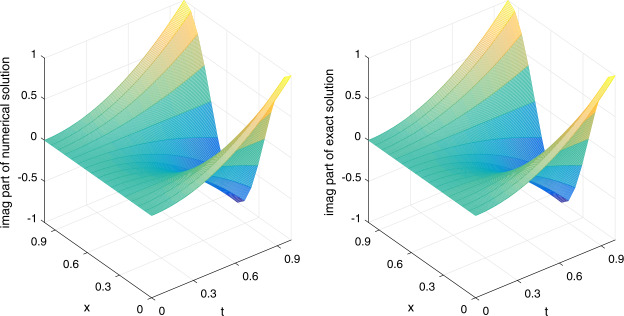
$Quintic non-polynomial spline for time-fractional nonlinear Schrödinger equation.$

查看原文本刊更多论文

Quintic non-polynomial spline for time-fractional nonlinear Schrödinger equation.

In this paper, we shall solve a time-fractional nonlinear Schrödinger equation by using the quintic non-polynomial spline and the L1 formula. The unconditional stability, unique solvability and convergence of our numerical scheme are proved by the Fourier method. It is shown that our method is sixth order accurate in the spatial dimension and $(2 - γ)$ th order accurate in the temporal dimension, where γ is the fractional order. The efficiency of the proposed numerical scheme is further illustrated by numerical experiments, meanwhile the simulation results indicate better performance over previous work in the literature.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Advances in Difference Equations 数学-数学

自引率

0.00%

发文量

审稿时长

4-8 weeks

期刊介绍： The theory of difference equations, the methods used, and their wide applications have advanced beyond their adolescent stage to occupy a central position in applicable analysis. In fact, in the last 15 years, the proliferation of the subject has been witnessed by hundreds of research articles, several monographs, many international conferences, and numerous special sessions. The theory of differential and difference equations forms two extreme representations of real world problems. For example, a simple population model when represented as a differential equation shows the good behavior of solutions whereas the corresponding discrete analogue shows the chaotic behavior. The actual behavior of the population is somewhere in between. The aim of Advances in Difference Equations is to report mainly the new developments in the field of difference equations, and their applications in all fields. We will also consider research articles emphasizing the qualitative behavior of solutions of ordinary, partial, delay, fractional, abstract, stochastic, fuzzy, and set-valued differential equations. Advances in Difference Equations will accept high-quality articles containing original research results and survey articles of exceptional merit.