接触者追踪对COVID-19传播影响的建模

IF 4.1 3区数学 Q1 Mathematics

Advances in Difference Equations Pub Date : 2020-01-01 Epub Date: 2020-09-21 DOI:10.1186/s13662-020-02972-8

Ali Traoré, Fourtoua Victorien Konané

{"title":"接触者追踪对COVID-19传播影响的建模","authors":"Ali Traoré, Fourtoua Victorien Konané","doi":"10.1186/s13662-020-02972-8","DOIUrl":null,"url":null,"abstract":"In this paper, a mathematical model for COVID-19 that involves contact tracing is studied. The contact tracing-induced reproduction number <math><msub><mi>R</mi> <mi>q</mi></msub> </math> and equilibrium for the model are determined and stabilities are examined. The global stabilities results are achieved by constructing Lyapunov functions. The contact tracing-induced reproduction number <math><msub><mi>R</mi> <mi>q</mi></msub> </math> is compared with the basic reproduction number <math><msub><mi>R</mi> <mn>0</mn></msub> </math> for the model in the absence of any intervention to assess the possible benefits of the contact tracing strategy.","PeriodicalId":53311,"journal":{"name":"Advances in Difference Equations","volume":null,"pages":null},"PeriodicalIF":4.1000,"publicationDate":"2020-01-01","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"https://sci-hub-pdf.com/10.1186/s13662-020-02972-8","citationCount":"1","resultStr":"{\"title\":\"Modeling the effects of contact tracing on COVID-19 transmission.\",\"authors\":\"Ali Traoré, Fourtoua Victorien Konané\",\"doi\":\"10.1186/s13662-020-02972-8\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"In this paper, a mathematical model for COVID-19 that involves contact tracing is studied. The contact tracing-induced reproduction number <math><msub><mi>R</mi> <mi>q</mi></msub> </math> and equilibrium for the model are determined and stabilities are examined. The global stabilities results are achieved by constructing Lyapunov functions. The contact tracing-induced reproduction number <math><msub><mi>R</mi> <mi>q</mi></msub> </math> is compared with the basic reproduction number <math><msub><mi>R</mi> <mn>0</mn></msub> </math> for the model in the absence of any intervention to assess the possible benefits of the contact tracing strategy.\",\"PeriodicalId\":53311,\"journal\":{\"name\":\"Advances in Difference Equations\",\"volume\":null,\"pages\":null},\"PeriodicalIF\":4.1000,\"publicationDate\":\"2020-01-01\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"https://sci-hub-pdf.com/10.1186/s13662-020-02972-8\",\"citationCount\":\"1\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Advances in Difference Equations\",\"FirstCategoryId\":\"100\",\"ListUrlMain\":\"https://doi.org/10.1186/s13662-020-02972-8\",\"RegionNum\":3,\"RegionCategory\":\"数学\",\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"2020/9/21 0:00:00\",\"PubModel\":\"Epub\",\"JCR\":\"Q1\",\"JCRName\":\"Mathematics\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Advances in Difference Equations","FirstCategoryId":"100","ListUrlMain":"https://doi.org/10.1186/s13662-020-02972-8","RegionNum":3,"RegionCategory":"数学","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"2020/9/21 0:00:00","PubModel":"Epub","JCR":"Q1","JCRName":"Mathematics","Score":null,"Total":0}

引用次数: 1

摘要

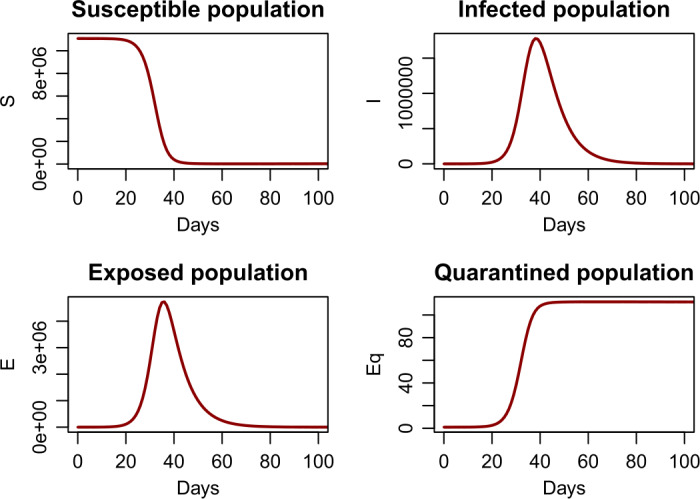
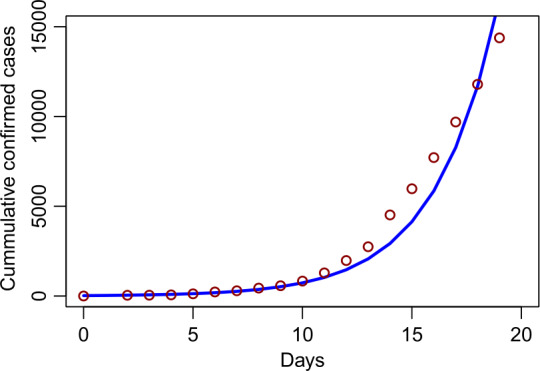
本文研究了涉及接触者追踪的COVID-19数学模型。确定了模型的接触跟踪诱导再现数rq和平衡点，并检验了模型的稳定性。通过构造Lyapunov函数得到全局稳定性结果。在没有任何干预的情况下，将接触追踪诱导的繁殖数rq与模型的基本繁殖数r0进行比较，以评估接触追踪策略可能带来的效益。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

Modeling the effects of contact tracing on COVID-19 transmission.

查看原文本刊更多论文

Modeling the effects of contact tracing on COVID-19 transmission.

In this paper, a mathematical model for COVID-19 that involves contact tracing is studied. The contact tracing-induced reproduction number $R_{q}$ and equilibrium for the model are determined and stabilities are examined. The global stabilities results are achieved by constructing Lyapunov functions. The contact tracing-induced reproduction number $R_{q}$ is compared with the basic reproduction number $R_{0}$ for the model in the absence of any intervention to assess the possible benefits of the contact tracing strategy.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Advances in Difference Equations 数学-数学

自引率

0.00%

发文量

审稿时长

4-8 weeks

期刊介绍： The theory of difference equations, the methods used, and their wide applications have advanced beyond their adolescent stage to occupy a central position in applicable analysis. In fact, in the last 15 years, the proliferation of the subject has been witnessed by hundreds of research articles, several monographs, many international conferences, and numerous special sessions. The theory of differential and difference equations forms two extreme representations of real world problems. For example, a simple population model when represented as a differential equation shows the good behavior of solutions whereas the corresponding discrete analogue shows the chaotic behavior. The actual behavior of the population is somewhere in between. The aim of Advances in Difference Equations is to report mainly the new developments in the field of difference equations, and their applications in all fields. We will also consider research articles emphasizing the qualitative behavior of solutions of ordinary, partial, delay, fractional, abstract, stochastic, fuzzy, and set-valued differential equations. Advances in Difference Equations will accept high-quality articles containing original research results and survey articles of exceptional merit.