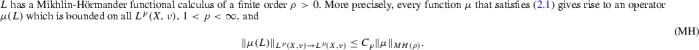
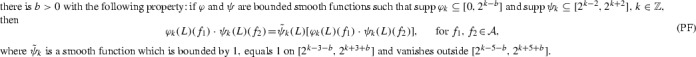
Approaching Bilinear Multipliers via a Functional Calculus.

We propose a framework for bilinear multiplier operators defined via the (bivariate) spectral theorem. Under this framework, we prove Coifman-Meyer type multiplier theorems and fractional Leibniz rules. Our theory applies to bilinear multipliers associated with the discrete Laplacian on $Z^d,$ general bi-radial bilinear Dunkl multipliers, and to bilinear multipliers associated with the Jacobi expansions.