λ-Bernstein-Kantorovich型二元张量积的G -B - S算子的混合型逼近。

IF 1.6 3区数学 Q1 Mathematics

Journal of Inequalities and Applications Pub Date : 2018-01-01 Epub Date: 2018-10-01 DOI:10.1186/s13660-018-1862-0

Qing-Bo Cai, Guorong Zhou

{"title":"λ-Bernstein-Kantorovich型二元张量积的G -B - S算子的混合型逼近。","authors":"Qing-Bo Cai, Guorong Zhou","doi":"10.1186/s13660-018-1862-0","DOIUrl":null,"url":null,"abstract":"In this paper, we introduce a family of <math><mi>G</mi> <mi>B</mi> <mi>S</mi></math> operators of bivariate tensor product of λ-Bernstein-Kantorovich type. We estimate the rate of convergence of such operators for B-continuous and B-differentiable functions by using the mixed modulus of smoothness, establish the Voronovskaja type asymptotic formula for the bivariate λ-Bernstein-Kantorovich operators, as well as give some examples and their graphs to show the effect of convergence.","PeriodicalId":49163,"journal":{"name":"Journal of Inequalities and Applications","volume":"2018 1","pages":"268"},"PeriodicalIF":1.6000,"publicationDate":"2018-01-01","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"https://sci-hub-pdf.com/10.1186/s13660-018-1862-0","citationCount":"9","resultStr":"{\"title\":\"<ArticleTitle xmlns:ns0=\\\"http://www.w3.org/1998/Math/MathML\\\">Blending type approximation by <ns0:math><ns0:mi>G</ns0:mi> <ns0:mi>B</ns0:mi> <ns0:mi>S</ns0:mi></ns0:math> operators of bivariate tensor product of λ-Bernstein-Kantorovich type.\",\"authors\":\"Qing-Bo Cai, Guorong Zhou\",\"doi\":\"10.1186/s13660-018-1862-0\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"In this paper, we introduce a family of <math><mi>G</mi> <mi>B</mi> <mi>S</mi></math> operators of bivariate tensor product of λ-Bernstein-Kantorovich type. We estimate the rate of convergence of such operators for B-continuous and B-differentiable functions by using the mixed modulus of smoothness, establish the Voronovskaja type asymptotic formula for the bivariate λ-Bernstein-Kantorovich operators, as well as give some examples and their graphs to show the effect of convergence.\",\"PeriodicalId\":49163,\"journal\":{\"name\":\"Journal of Inequalities and Applications\",\"volume\":\"2018 1\",\"pages\":\"268\"},\"PeriodicalIF\":1.6000,\"publicationDate\":\"2018-01-01\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"https://sci-hub-pdf.com/10.1186/s13660-018-1862-0\",\"citationCount\":\"9\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Journal of Inequalities and Applications\",\"FirstCategoryId\":\"100\",\"ListUrlMain\":\"https://doi.org/10.1186/s13660-018-1862-0\",\"RegionNum\":3,\"RegionCategory\":\"数学\",\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"2018/10/1 0:00:00\",\"PubModel\":\"Epub\",\"JCR\":\"Q1\",\"JCRName\":\"Mathematics\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Journal of Inequalities and Applications","FirstCategoryId":"100","ListUrlMain":"https://doi.org/10.1186/s13660-018-1862-0","RegionNum":3,"RegionCategory":"数学","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"2018/10/1 0:00:00","PubModel":"Epub","JCR":"Q1","JCRName":"Mathematics","Score":null,"Total":0}

引用次数: 9

摘要

本文引入了λ-Bernstein-Kantorovich型二元张量积的G B S算子族。利用光滑的混合模估计了b -连续函数和b -可微函数的这类算子的收敛速度，建立了二元λ-Bernstein-Kantorovich算子的Voronovskaja型渐近公式，并给出了一些例子和图来说明收敛效果。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

<ArticleTitle xmlns:ns0="http://www.w3.org/1998/Math/MathML">Blending type approximation by <ns0:math><ns0:mi>G</ns0:mi> <ns0:mi>B</ns0:mi> <ns0:mi>S</ns0:mi></ns0:math> operators of bivariate tensor product of λ-Bernstein-Kantorovich type.

查看原文本刊更多论文

Blending type approximation by G B S operators of bivariate tensor product of λ-Bernstein-Kantorovich type.

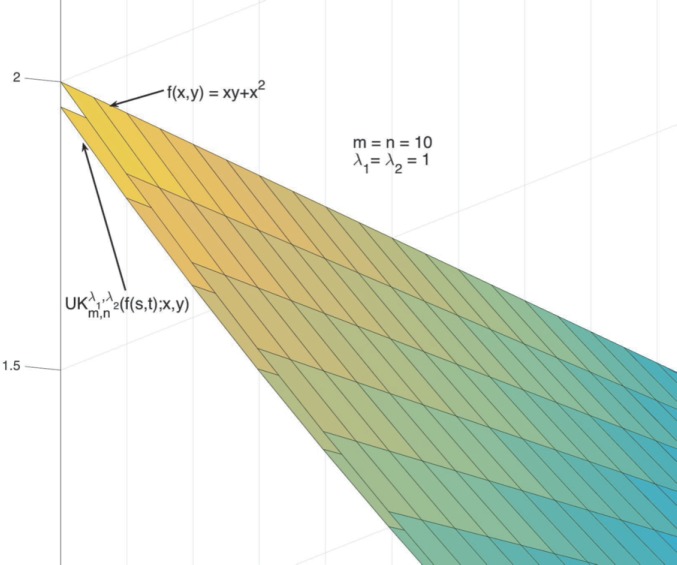
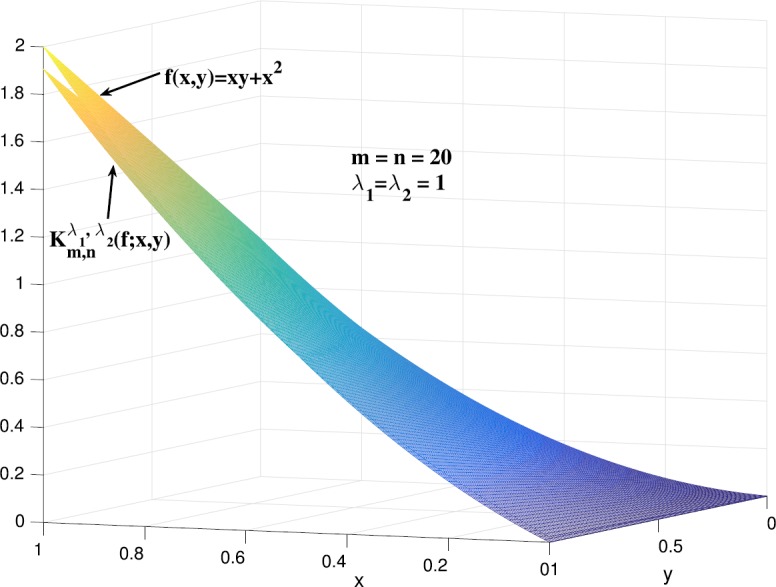
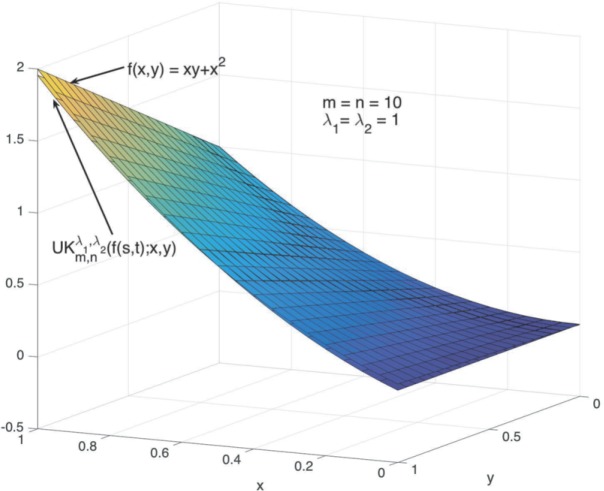
In this paper, we introduce a family of $G B S$ operators of bivariate tensor product of λ-Bernstein-Kantorovich type. We estimate the rate of convergence of such operators for B-continuous and B-differentiable functions by using the mixed modulus of smoothness, establish the Voronovskaja type asymptotic formula for the bivariate λ-Bernstein-Kantorovich operators, as well as give some examples and their graphs to show the effect of convergence.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Journal of Inequalities and Applications MATHEMATICS, APPLIED-MATHEMATICS

CiteScore

3.30

自引率

6.20%

发文量

136

审稿时长

3 months

期刊介绍： The aim of this journal is to provide a multi-disciplinary forum of discussion in mathematics and its applications in which the essentiality of inequalities is highlighted. This Journal accepts high quality articles containing original research results and survey articles of exceptional merit. Subject matters should be strongly related to inequalities, such as, but not restricted to, the following: inequalities in analysis, inequalities in approximation theory, inequalities in combinatorics, inequalities in economics, inequalities in geometry, inequalities in mechanics, inequalities in optimization, inequalities in stochastic analysis and applications.