扩散耦合Lotka-Volterra系统元模型的高阶孤立解。

IF 4.1 3区数学 Q1 Mathematics

Advances in Difference Equations Pub Date : 2021-01-01 Epub Date: 2021-02-25 DOI:10.1186/s13662-021-03300-4

Inga Timofejeva, Tadas Telksnys, Zenonas Navickas, Romas Marcinkevicius, Minvydas Ragulskis

{"title":"扩散耦合Lotka-Volterra系统元模型的高阶孤立解。","authors":"Inga Timofejeva, Tadas Telksnys, Zenonas Navickas, Romas Marcinkevicius, Minvydas Ragulskis","doi":"10.1186/s13662-021-03300-4","DOIUrl":null,"url":null,"abstract":"A meta-model of diffusively coupled Lotka-Volterra systems used to model various biomedical phenomena is considered in this paper. Necessary and sufficient conditions for the existence of nth order solitary solutions are derived via a modified inverse balancing technique. It is shown that as the highest possible solitary solution order n is increased, the number of nonzero solution parameter values remains constant for solitary solutions of order <math><mi>n</mi> <mo>></mo> <mn>3</mn></math> . Analytical and computational experiments are used to illustrate the obtained results.","PeriodicalId":53311,"journal":{"name":"Advances in Difference Equations","volume":null,"pages":null},"PeriodicalIF":4.1000,"publicationDate":"2021-01-01","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"https://sci-hub-pdf.com/10.1186/s13662-021-03300-4","citationCount":"1","resultStr":"{\"title\":\"Higher order solitary solutions to the meta-model of diffusively coupled Lotka-Volterra systems.\",\"authors\":\"Inga Timofejeva, Tadas Telksnys, Zenonas Navickas, Romas Marcinkevicius, Minvydas Ragulskis\",\"doi\":\"10.1186/s13662-021-03300-4\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"A meta-model of diffusively coupled Lotka-Volterra systems used to model various biomedical phenomena is considered in this paper. Necessary and sufficient conditions for the existence of nth order solitary solutions are derived via a modified inverse balancing technique. It is shown that as the highest possible solitary solution order n is increased, the number of nonzero solution parameter values remains constant for solitary solutions of order <math><mi>n</mi> <mo>></mo> <mn>3</mn></math> . Analytical and computational experiments are used to illustrate the obtained results.\",\"PeriodicalId\":53311,\"journal\":{\"name\":\"Advances in Difference Equations\",\"volume\":null,\"pages\":null},\"PeriodicalIF\":4.1000,\"publicationDate\":\"2021-01-01\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"https://sci-hub-pdf.com/10.1186/s13662-021-03300-4\",\"citationCount\":\"1\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Advances in Difference Equations\",\"FirstCategoryId\":\"100\",\"ListUrlMain\":\"https://doi.org/10.1186/s13662-021-03300-4\",\"RegionNum\":3,\"RegionCategory\":\"数学\",\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"2021/2/25 0:00:00\",\"PubModel\":\"Epub\",\"JCR\":\"Q1\",\"JCRName\":\"Mathematics\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Advances in Difference Equations","FirstCategoryId":"100","ListUrlMain":"https://doi.org/10.1186/s13662-021-03300-4","RegionNum":3,"RegionCategory":"数学","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"2021/2/25 0:00:00","PubModel":"Epub","JCR":"Q1","JCRName":"Mathematics","Score":null,"Total":0}

引用次数: 1

摘要

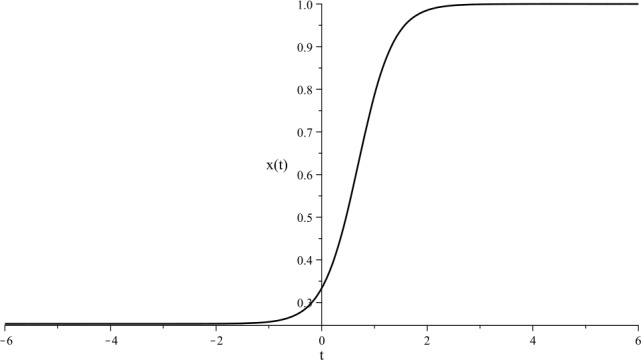
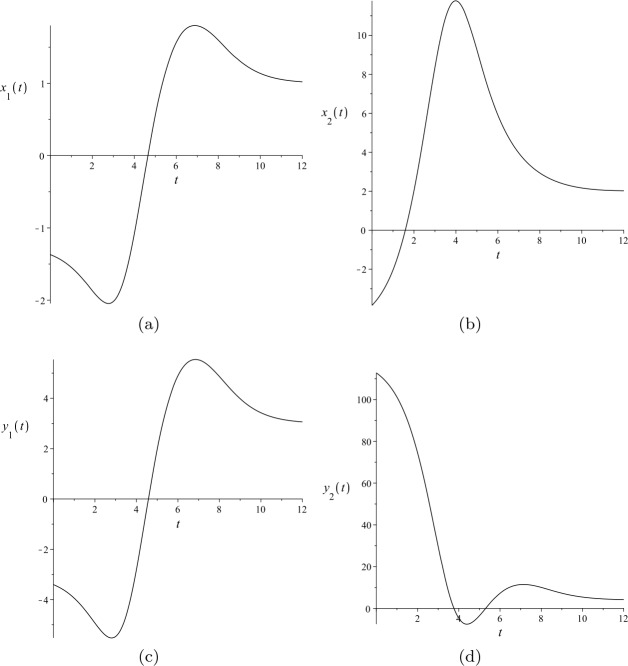
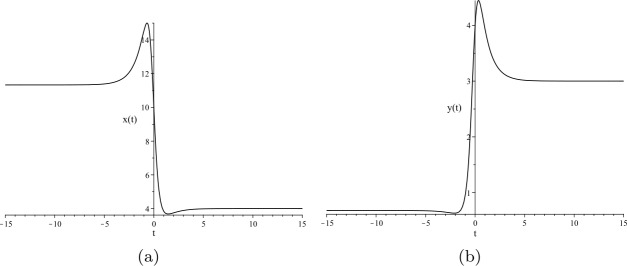
本文考虑了用于模拟各种生物医学现象的扩散耦合Lotka-Volterra系统的元模型。利用一种改进的逆平衡技术，得到了n阶孤立解存在的充分必要条件。结果表明，随着最高可能孤立解阶n的增加，对于n > 3阶的孤立解，非零解参数值的个数保持不变。通过分析和计算实验对所得结果进行了说明。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

Higher order solitary solutions to the meta-model of diffusively coupled Lotka-Volterra systems.

查看原文本刊更多论文

Higher order solitary solutions to the meta-model of diffusively coupled Lotka-Volterra systems.

A meta-model of diffusively coupled Lotka-Volterra systems used to model various biomedical phenomena is considered in this paper. Necessary and sufficient conditions for the existence of nth order solitary solutions are derived via a modified inverse balancing technique. It is shown that as the highest possible solitary solution order n is increased, the number of nonzero solution parameter values remains constant for solitary solutions of order $n > 3$ . Analytical and computational experiments are used to illustrate the obtained results.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Advances in Difference Equations 数学-数学

自引率

0.00%

发文量

审稿时长

4-8 weeks

期刊介绍： The theory of difference equations, the methods used, and their wide applications have advanced beyond their adolescent stage to occupy a central position in applicable analysis. In fact, in the last 15 years, the proliferation of the subject has been witnessed by hundreds of research articles, several monographs, many international conferences, and numerous special sessions. The theory of differential and difference equations forms two extreme representations of real world problems. For example, a simple population model when represented as a differential equation shows the good behavior of solutions whereas the corresponding discrete analogue shows the chaotic behavior. The actual behavior of the population is somewhere in between. The aim of Advances in Difference Equations is to report mainly the new developments in the field of difference equations, and their applications in all fields. We will also consider research articles emphasizing the qualitative behavior of solutions of ordinary, partial, delay, fractional, abstract, stochastic, fuzzy, and set-valued differential equations. Advances in Difference Equations will accept high-quality articles containing original research results and survey articles of exceptional merit.