偶然性离散复合体具有增强的规律性。

IF 1.3 2区数学 Q1 MATHEMATICS

Calcolo Pub Date : 2025-01-01 Epub Date: 2025-10-15 DOI:10.1007/s10092-025-00665-w

Daniele A Di Pietro, Marien Hanot, Marwa Salah

{"title":"偶然性离散复合体具有增强的规律性。","authors":"Daniele A Di Pietro, Marien Hanot, Marwa Salah","doi":"10.1007/s10092-025-00665-w","DOIUrl":null,"url":null,"abstract":"In this work we address the problem of finding serendipity versions of approximate de Rham complexes with enhanced regularity. The starting point is a new abstract construction of general scope which, given three complexes linked by extension and reduction maps, generates a fourth complex with cohomology isomorphic to the former three. This construction is used to devise new serendipity versions of rot-rot and Stokes complexes derived in the Discrete de Rham spirit.","PeriodicalId":9522,"journal":{"name":"Calcolo","volume":"62 4","pages":"41"},"PeriodicalIF":1.3000,"publicationDate":"2025-01-01","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"https://www.ncbi.nlm.nih.gov/pmc/articles/PMC12528296/pdf/","citationCount":"0","resultStr":"{\"title\":\"Serendipity discrete complexes with enhanced regularity.\",\"authors\":\"Daniele A Di Pietro, Marien Hanot, Marwa Salah\",\"doi\":\"10.1007/s10092-025-00665-w\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"In this work we address the problem of finding serendipity versions of approximate de Rham complexes with enhanced regularity. The starting point is a new abstract construction of general scope which, given three complexes linked by extension and reduction maps, generates a fourth complex with cohomology isomorphic to the former three. This construction is used to devise new serendipity versions of rot-rot and Stokes complexes derived in the Discrete de Rham spirit.\",\"PeriodicalId\":9522,\"journal\":{\"name\":\"Calcolo\",\"volume\":\"62 4\",\"pages\":\"41\"},\"PeriodicalIF\":1.3000,\"publicationDate\":\"2025-01-01\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"https://www.ncbi.nlm.nih.gov/pmc/articles/PMC12528296/pdf/\",\"citationCount\":\"0\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Calcolo\",\"FirstCategoryId\":\"100\",\"ListUrlMain\":\"https://doi.org/10.1007/s10092-025-00665-w\",\"RegionNum\":2,\"RegionCategory\":\"数学\",\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"2025/10/15 0:00:00\",\"PubModel\":\"Epub\",\"JCR\":\"Q1\",\"JCRName\":\"MATHEMATICS\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Calcolo","FirstCategoryId":"100","ListUrlMain":"https://doi.org/10.1007/s10092-025-00665-w","RegionNum":2,"RegionCategory":"数学","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"2025/10/15 0:00:00","PubModel":"Epub","JCR":"Q1","JCRName":"MATHEMATICS","Score":null,"Total":0}

引用次数: 0

摘要

在这项工作中，我们解决了寻找具有增强规律性的近似德拉姆复合体的偶然版本的问题。本文的出发点是一个新的一般范围的抽象结构，给定三个由延约映射连接的复合体，生成与前三个复合体上同构的第四个复合体。这种结构被用来设计新的偶然版本的rot-rot和Stokes复合体，这些复合体来源于离散的德拉姆精神。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

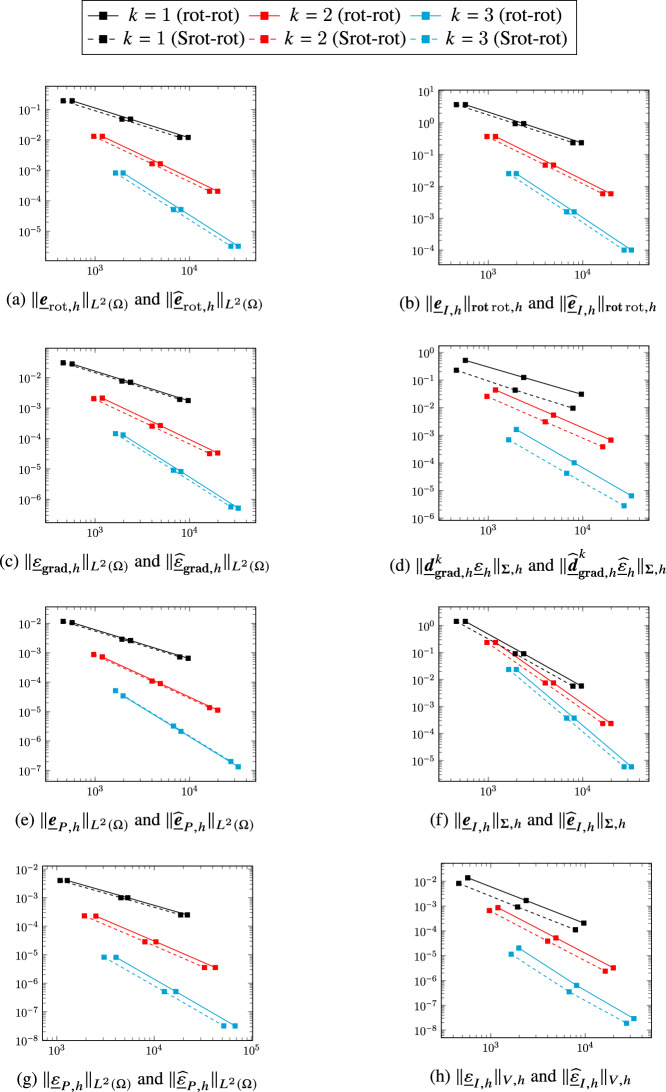
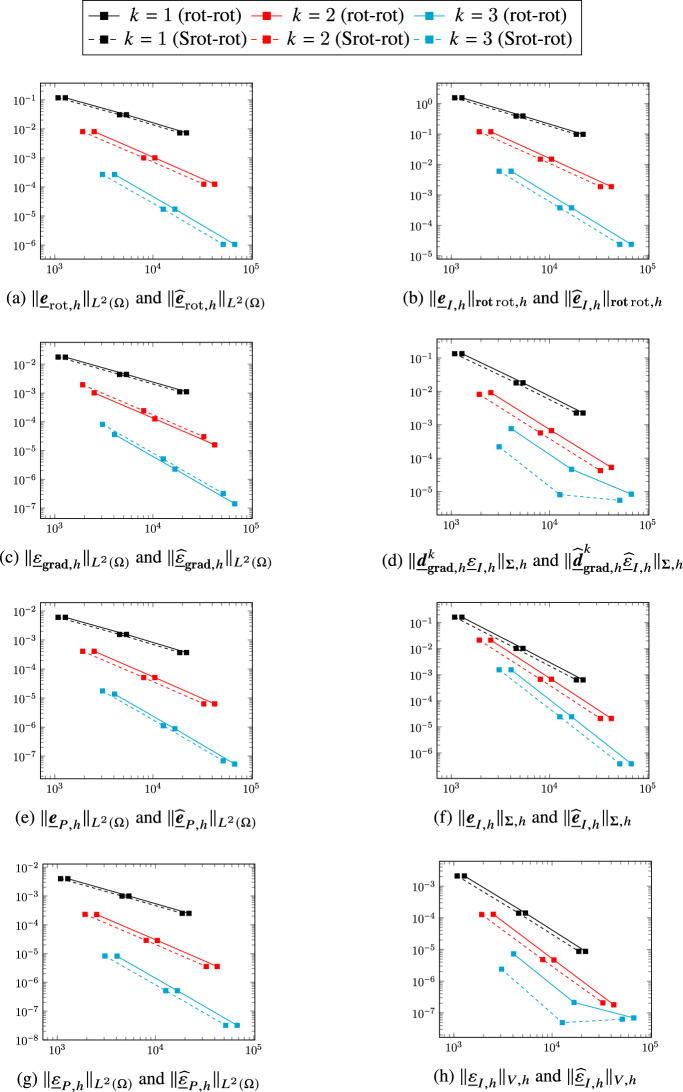
Serendipity discrete complexes with enhanced regularity.

查看原文本刊更多论文

Serendipity discrete complexes with enhanced regularity.

In this work we address the problem of finding serendipity versions of approximate de Rham complexes with enhanced regularity. The starting point is a new abstract construction of general scope which, given three complexes linked by extension and reduction maps, generates a fourth complex with cohomology isomorphic to the former three. This construction is used to devise new serendipity versions of rot-rot and Stokes complexes derived in the Discrete de Rham spirit.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Calcolo 数学-数学

CiteScore

2.40

自引率

11.80%

发文量

审稿时长

>12 weeks

期刊介绍： Calcolo is a quarterly of the Italian National Research Council, under the direction of the Institute for Informatics and Telematics in Pisa. Calcolo publishes original contributions in English on Numerical Analysis and its Applications, and on the Theory of Computation. The main focus of the journal is on Numerical Linear Algebra, Approximation Theory and its Applications, Numerical Solution of Differential and Integral Equations, Computational Complexity, Algorithmics, Mathematical Aspects of Computer Science, Optimization Theory. Expository papers will also appear from time to time as an introduction to emerging topics in one of the above mentioned fields. There will be a "Report" section, with abstracts of PhD Theses, news and reports from conferences and book reviews. All submissions will be carefully refereed.