含损伤有限应变粘弹性的通用UMAT
IF 3.5
3区 工程技术
Q1 MATHEMATICS, APPLIED
引用次数: 0
摘要
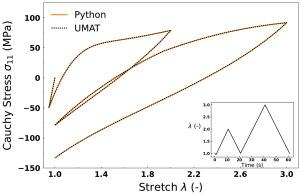
给出了具有应变软化和温度依赖性的一般有限应变粘弹性材料的UMAT。该模型建立在Reese和Govindjee(1998)的热力学一致公式的基础上,扩展到支持依赖于不变量I1和I2的一般偏应变能函数,以及影响偏应变和静水响应的各向同性损伤机制。本文首先概述了建模假设,并描述了数值实现,包括对一般应变能函数的灵活结合的修改,与混合有限元的兼容性,以及UMAT子程序的结构。通过一系列的单轴和剪切基准试验,在各种荷载条件下验证了该实现。最后,一个涉及细长矩形杆的循环扭转的结构模拟证实了一致切线模量的正确实现。所提出的UMAT是通用的,适用于广泛的材料,包括具有马林斯软化的准不可压缩橡胶和由于基质填料脱粘而遭受体积破坏的固体推进剂。本文章由计算机程序翻译,如有差异,请以英文原文为准。
A general UMAT for finite-strain viscoelasticity with damage
A UMAT for general finite-strain viscoelastic materials exhibiting strain softening and temperature dependence is presented and shared. The model builds on the thermodynamically consistent formulation of Reese and Govindjee (1998), extended to support a general deviatoric strain energy function depending on the invariants and , as well as isotropic damage mechanisms affecting both deviatoric and hydrostatic responses. The paper first outlines the modeling assumptions and describes the numerical implementation, including modifications for the flexible incorporation of general strain energy functions, compatibility with hybrid finite elements, and the structure of the UMAT subroutine. The implementation is validated through a series of uniaxial and shear benchmark tests under various loading conditions. Finally, a structural simulation involving the cyclic torsion of a slender rectangular bar confirms the correct implementation of the consistent tangent modulus. The proposed UMAT is versatile and applicable to a broad class of materials, including quasi-incompressible rubbers exhibiting Mullins softening and solid propellants undergoing volumetric damage due to matrix-filler debonding.
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊
CiteScore
4.80
自引率
3.20%
发文量
92
审稿时长
27 days
期刊介绍:
The aim of this journal is to provide ideas and information involving the use of the finite element method and its variants, both in scientific inquiry and in professional practice. The scope is intentionally broad, encompassing use of the finite element method in engineering as well as the pure and applied sciences. The emphasis of the journal will be the development and use of numerical procedures to solve practical problems, although contributions relating to the mathematical and theoretical foundations and computer implementation of numerical methods are likewise welcomed. Review articles presenting unbiased and comprehensive reviews of state-of-the-art topics will also be accommodated.

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


