相对Gromov-Witten和最大接触二次曲线
IF 0.5
4区 数学
Q3 MATHEMATICS
引用次数: 0
摘要
讨论了在一点上具有最大接触阶的有理曲线的相对Gromov-Witten不变量的一些性质。我们计算任意光滑平面曲线的Cayley六分圆锥数。特别地,我们计算了曲折线的双重覆盖在一定程度上相对于曲线的两个相对Gromov-Witten不变量的贡献。本文章由计算机程序翻译,如有差异,请以英文原文为准。
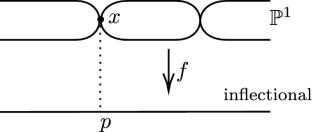
Relative Gromov–Witten and maximal contact conics
We discuss some properties of the relative Gromov–Witten invariants counting rational curves with maximal contact order at one point. We compute the number of Cayley’s sextactic conics to any smooth plane curve. In particular, we compute the contribution, from double covers of inflectional lines, to a certain degree two relative Gromov–Witten invariant relative to the curve.
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊

Archiv der Mathematik
数学-数学
CiteScore
1.10
自引率
0.00%
发文量
117
审稿时长
4-8 weeks
期刊介绍:
Archiv der Mathematik (AdM) publishes short high quality research papers in every area of mathematics which are not overly technical in nature and addressed to a broad readership.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


