亚稳态的简单有限维模型

IF 0.4 4区物理与天体物理 Q4 PHYSICS, MULTIDISCIPLINARY

Moscow University Physics Bulletin Pub Date : 2025-07-13 DOI:10.3103/S0027134925700298

A. I. Dubikovsky, P. K. Silaev

{"title":"亚稳态的简单有限维模型","authors":"A. I. Dubikovsky, P. K. Silaev","doi":"10.3103/S0027134925700298","DOIUrl":null,"url":null,"abstract":"<p>We have constructed an approximate analytical solution to the spectral problem for a finite-dimensional matrix of a special form, which proves to be a very simple and sufficiently satisfactory model of the metastable state. This model reproduces most of the characteristic properties of the metastable state, including the line shape, decay dynamics, and density of states. The accuracy of the approximate analytical solution was verified through direct numerical calculations. The proposed model represents a finite-dimensional analog of the Fano formalism.</p>","PeriodicalId":711,"journal":{"name":"Moscow University Physics Bulletin","volume":"80 2","pages":"226 - 235"},"PeriodicalIF":0.4000,"publicationDate":"2025-07-13","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"","citationCount":"0","resultStr":"{\"title\":\"A Simple Finite-Dimensional Model of the Metastable State\",\"authors\":\"A. I. Dubikovsky, P. K. Silaev\",\"doi\":\"10.3103/S0027134925700298\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"<p>We have constructed an approximate analytical solution to the spectral problem for a finite-dimensional matrix of a special form, which proves to be a very simple and sufficiently satisfactory model of the metastable state. This model reproduces most of the characteristic properties of the metastable state, including the line shape, decay dynamics, and density of states. The accuracy of the approximate analytical solution was verified through direct numerical calculations. The proposed model represents a finite-dimensional analog of the Fano formalism.</p>\",\"PeriodicalId\":711,\"journal\":{\"name\":\"Moscow University Physics Bulletin\",\"volume\":\"80 2\",\"pages\":\"226 - 235\"},\"PeriodicalIF\":0.4000,\"publicationDate\":\"2025-07-13\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"\",\"citationCount\":\"0\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Moscow University Physics Bulletin\",\"FirstCategoryId\":\"101\",\"ListUrlMain\":\"https://link.springer.com/article/10.3103/S0027134925700298\",\"RegionNum\":4,\"RegionCategory\":\"物理与天体物理\",\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"\",\"PubModel\":\"\",\"JCR\":\"Q4\",\"JCRName\":\"PHYSICS, MULTIDISCIPLINARY\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Moscow University Physics Bulletin","FirstCategoryId":"101","ListUrlMain":"https://link.springer.com/article/10.3103/S0027134925700298","RegionNum":4,"RegionCategory":"物理与天体物理","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q4","JCRName":"PHYSICS, MULTIDISCIPLINARY","Score":null,"Total":0}

引用次数: 0

摘要

我们构造了一类特殊形式的有限维矩阵的谱问题的近似解析解，证明了它是一个非常简单和足够令人满意的亚稳态模型。该模型再现了亚稳态的大部分特性，包括线形、衰变动力学和态密度。通过直接数值计算验证了近似解析解的准确性。所提出的模型代表了法诺形式主义的有限维模拟。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

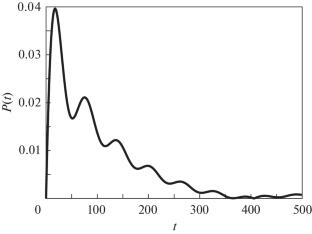
A Simple Finite-Dimensional Model of the Metastable State

查看原文本刊更多论文

A Simple Finite-Dimensional Model of the Metastable State

We have constructed an approximate analytical solution to the spectral problem for a finite-dimensional matrix of a special form, which proves to be a very simple and sufficiently satisfactory model of the metastable state. This model reproduces most of the characteristic properties of the metastable state, including the line shape, decay dynamics, and density of states. The accuracy of the approximate analytical solution was verified through direct numerical calculations. The proposed model represents a finite-dimensional analog of the Fano formalism.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Moscow University Physics Bulletin PHYSICS, MULTIDISCIPLINARY-

CiteScore

0.70

自引率

0.00%

发文量

129

审稿时长

6-12 weeks

期刊介绍： Moscow University Physics Bulletin publishes original papers (reviews, articles, and brief communications) in the following fields of experimental and theoretical physics: theoretical and mathematical physics; physics of nuclei and elementary particles; radiophysics, electronics, acoustics; optics and spectroscopy; laser physics; condensed matter physics; chemical physics, physical kinetics, and plasma physics; biophysics and medical physics; astronomy, astrophysics, and cosmology; physics of the Earth’s, atmosphere, and hydrosphere.