Boussinesq - Rayleigh-Taylor湍流对初始条件的后期敏感性模拟
IF 2.9
3区 数学
Q1 MATHEMATICS, APPLIED
引用次数: 0
摘要
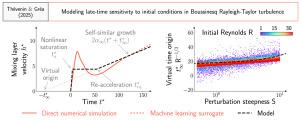
本文阐明了初始条件对布辛内斯克-瑞利-泰勒湍流的影响。它建立在thsamvenin等人(2025)的相关论文的基础上,该论文介绍了一个物理信息的神经网络,该网络可以有效地将动力学外推到非常晚的时间和看不见的初始条件,超出了直接数值模拟的范围。本论文的重点是自相似机制,并结合了机器学习、基于方差的敏感性分析和理论,以提供对初始条件的后期依赖性的强大理解。特别强调的是虚拟时间原点,它显示出与初始雷诺数、摄动陡度和带宽数强烈变化。我们开发了一个基于瑞利-泰勒混合层现象学的分析模型来解释这种依赖关系,并给出了虚拟时间起源的准确预测。结果表明,初始扰动达到非线性饱和越早,混合层重新加速越早,虚时间原点越大。本文章由计算机程序翻译,如有差异,请以英文原文为准。
Modeling late-time sensitivity to initial conditions in Boussinesq Rayleigh–Taylor turbulence
This article sheds light on the influence of initial conditions in Boussinesq Rayleigh–Taylor turbulence. It builds on the related paper from Thévenin et al. (2025), which introduces a physics-informed neural network that effectively extrapolates the dynamics to very late times and unseen initial conditions, beyond the reach of direct numerical simulations. The present paper focuses on the self-similar regime and combines machine learning, variance-based sensitivity analysis and theory to provide a robust understanding of the late-time dependency on initial conditions. Particular emphasis is placed on the virtual time origin, which is shown to strongly vary with the initial Reynolds, perturbation steepness and bandwidth numbers. We develop an analytical model based on the phenomenology of Rayleigh–Taylor mixing layers to explain most of this dependency and give accurate predictions of the virtual time origin. It turns out that when the initial perturbation reaches nonlinear saturation earlier, the mixing layer also re-accelerates earlier, while the virtual time origin is larger.
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊

Physica D: Nonlinear Phenomena
物理-物理:数学物理
CiteScore
7.30
自引率
7.50%
发文量
213
审稿时长
65 days
期刊介绍:
Physica D (Nonlinear Phenomena) publishes research and review articles reporting on experimental and theoretical works, techniques and ideas that advance the understanding of nonlinear phenomena. Topics encompass wave motion in physical, chemical and biological systems; physical or biological phenomena governed by nonlinear field equations, including hydrodynamics and turbulence; pattern formation and cooperative phenomena; instability, bifurcations, chaos, and space-time disorder; integrable/Hamiltonian systems; asymptotic analysis and, more generally, mathematical methods for nonlinear systems.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


