一种物理引导的模拟变阶分数阶混沌金融模型的深度神经网络方法
IF 3
3区 工程技术
Q2 ENGINEERING, ELECTRICAL & ELECTRONIC
引用次数: 0
摘要
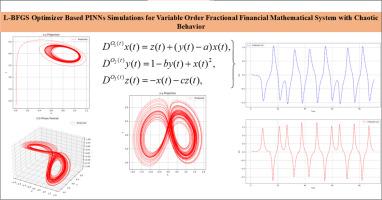
常数分数阶数学模型强调了现实系统的关键方面,但当科学家开始探索变阶模型时,才出现了重大进展。本研究具有两个主要的重要方面,首先,它解决了一个变阶分数金融数学系统,其次,它使用pinn方法解决了这个模型。目的利用有限记忆Broyden-Fletcher-Goldfarb-Shanno (L-BFGS)优化器为基础的物理信息神经网络(pinn),探讨变阶分数金融数学模型的数值解。该框架利用Caputo变阶分数阶微分算子捕捉了分数阶金融模型固有的非线性、复杂性和记忆依赖性特征。该方案保证了快速收敛性,并提供了变分数阶混沌轨迹的鲁棒逼近。这项研究更好地反映了金融体系的复杂性。讨论了整数和变阶分数系统的两种主要情况。此外,变量情况有三种子情况,具有不同的功能。对于每种情况,显示不同的图,显示混沌行为。本研究的重点是一个广义的变序分数金融体系,它包含了关键的经济成分:利率、投资需求和价格指数。结果表明,该方法的收敛阶与理论预期一致。我们的研究结果表明,在案例2c中使用的函数(O3(t)=(115)esin(125)t+0.76)最有效地捕捉了真实金融动态的复杂性和非平稳性。本文章由计算机程序翻译,如有差异,请以英文原文为准。
A physics-guided deep neural network approach for simulating variable-order fractional chaotic financial models
Significance
Constant fractional-order mathematical models have highlighted key aspects of real-life systems, but a major advancement occurred when scientists began exploring variable-order models. This study holds two main considerable aspects, firstly, it addresses a variable-order fractional financial mathematical system, and secondly, it solves this model using the PINNs methodology.
Purpose
This study explores the numerical solution of variable order fractional financial mathematical model through Limited-memory Broyden–Fletcher–Goldfarb–Shanno (L-BFGS) optimizer-based Physics-Informed Neural Networks (PINNs). This framework captures the nonlinear, complex and memory-dependent features inherent in fractional financial model with Caputo variable-order fractional differential operator. This scheme ensures fast convergence and provides robust approximations of chaotic trajectories under varying fractional orders. This study shows better representation of the intricacies of financial systems. There are discussed two main cases of integer and variable order fractional system. Furthermore, there are three subcases of variable case with different functions. For each case different plots are displayed, which show chaotic behavior.
Findings
In this study, it is focused on a generalized variable-order fractional financial system that incorporates key economic components: interest rate, investment demand, and price index. Results confirm that the method achieves a convergence order consistent with theoretical expectations. Our findings suggest that the function employed in Case 2c, is the most effective in capturing the complex and non-stationary nature of real financial dynamics.
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊

Digital Signal Processing
工程技术-工程:电子与电气
CiteScore
5.30
自引率
17.20%
发文量
435
审稿时长
66 days
期刊介绍:
Digital Signal Processing: A Review Journal is one of the oldest and most established journals in the field of signal processing yet it aims to be the most innovative. The Journal invites top quality research articles at the frontiers of research in all aspects of signal processing. Our objective is to provide a platform for the publication of ground-breaking research in signal processing with both academic and industrial appeal.
The journal has a special emphasis on statistical signal processing methodology such as Bayesian signal processing, and encourages articles on emerging applications of signal processing such as:
• big data• machine learning• internet of things• information security• systems biology and computational biology,• financial time series analysis,• autonomous vehicles,• quantum computing,• neuromorphic engineering,• human-computer interaction and intelligent user interfaces,• environmental signal processing,• geophysical signal processing including seismic signal processing,• chemioinformatics and bioinformatics,• audio, visual and performance arts,• disaster management and prevention,• renewable energy,
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


