闵可夫斯基平面上的单色无限集。

IF 0.6 3区数学 Q4 COMPUTER SCIENCE, THEORY & METHODS

Discrete & Computational Geometry Pub Date : 2025-01-01 Epub Date: 2024-11-12 DOI:10.1007/s00454-024-00702-5

Nóra Frankl, Panna Gehér, Arsenii Sagdeev, Géza Tóth

{"title":"闵可夫斯基平面上的单色无限集。","authors":"Nóra Frankl, Panna Gehér, Arsenii Sagdeev, Géza Tóth","doi":"10.1007/s00454-024-00702-5","DOIUrl":null,"url":null,"abstract":"We prove that for any <math><msub><mi>ℓ</mi> <mi>p</mi></msub> </math> -norm in the plane with <math><mrow><mn>1</mn> <mo><</mo> <mi>p</mi> <mo><</mo> <mi>∞</mi></mrow> </math> and for every infinite <math><mrow><mi>M</mi> <mo>⊂</mo> <msup><mrow><mi>R</mi></mrow> <mn>2</mn></msup> </mrow> </math> , there exists a two-colouring of the plane such that no isometric copy of <math><mi>M</mi></math> is monochromatic. On the contrary, we show that for every polygonal norm (that is, the unit ball is a polygon) in the plane, there exists an infinite <math><mrow><mi>M</mi> <mo>⊂</mo> <msup><mrow><mi>R</mi></mrow> <mn>2</mn></msup> </mrow> </math> such that for every two-colouring of the plane there exists a monochromatic isometric copy of <math><mi>M</mi></math> .","PeriodicalId":50574,"journal":{"name":"Discrete & Computational Geometry","volume":"74 2","pages":"569-583"},"PeriodicalIF":0.6000,"publicationDate":"2025-01-01","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"https://www.ncbi.nlm.nih.gov/pmc/articles/PMC12449424/pdf/","citationCount":"0","resultStr":"{\"title\":\"Monochromatic Infinite Sets in Minkowski Planes.\",\"authors\":\"Nóra Frankl, Panna Gehér, Arsenii Sagdeev, Géza Tóth\",\"doi\":\"10.1007/s00454-024-00702-5\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"We prove that for any <math><msub><mi>ℓ</mi> <mi>p</mi></msub> </math> -norm in the plane with <math><mrow><mn>1</mn> <mo><</mo> <mi>p</mi> <mo><</mo> <mi>∞</mi></mrow> </math> and for every infinite <math><mrow><mi>M</mi> <mo>⊂</mo> <msup><mrow><mi>R</mi></mrow> <mn>2</mn></msup> </mrow> </math> , there exists a two-colouring of the plane such that no isometric copy of <math><mi>M</mi></math> is monochromatic. On the contrary, we show that for every polygonal norm (that is, the unit ball is a polygon) in the plane, there exists an infinite <math><mrow><mi>M</mi> <mo>⊂</mo> <msup><mrow><mi>R</mi></mrow> <mn>2</mn></msup> </mrow> </math> such that for every two-colouring of the plane there exists a monochromatic isometric copy of <math><mi>M</mi></math> .\",\"PeriodicalId\":50574,\"journal\":{\"name\":\"Discrete & Computational Geometry\",\"volume\":\"74 2\",\"pages\":\"569-583\"},\"PeriodicalIF\":0.6000,\"publicationDate\":\"2025-01-01\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"https://www.ncbi.nlm.nih.gov/pmc/articles/PMC12449424/pdf/\",\"citationCount\":\"0\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Discrete & Computational Geometry\",\"FirstCategoryId\":\"100\",\"ListUrlMain\":\"https://doi.org/10.1007/s00454-024-00702-5\",\"RegionNum\":3,\"RegionCategory\":\"数学\",\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"2024/11/12 0:00:00\",\"PubModel\":\"Epub\",\"JCR\":\"Q4\",\"JCRName\":\"COMPUTER SCIENCE, THEORY & METHODS\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Discrete & Computational Geometry","FirstCategoryId":"100","ListUrlMain":"https://doi.org/10.1007/s00454-024-00702-5","RegionNum":3,"RegionCategory":"数学","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"2024/11/12 0:00:00","PubModel":"Epub","JCR":"Q4","JCRName":"COMPUTER SCIENCE, THEORY & METHODS","Score":null,"Total":0}

引用次数: 0

摘要

我们证明，对于平面上的任意p模，在1 p∞上，对于每一个无限M∧R 2，存在平面的双着色，使得M的等距副本不存在单色。相反，我们证明，对于平面上的每一个多边形范数（即，单位球是一个多边形），存在一个无限的M∧R 2，使得对于平面的每一个两色都存在M的单色等距副本。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

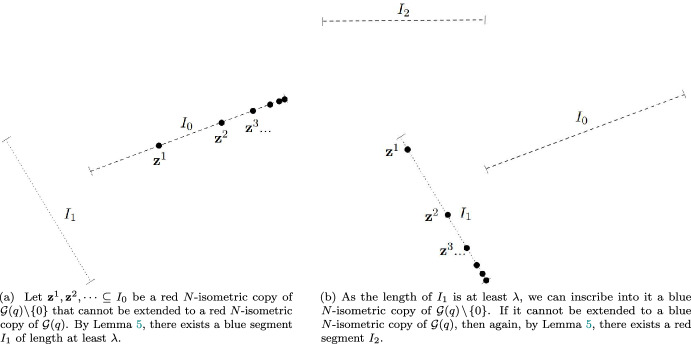
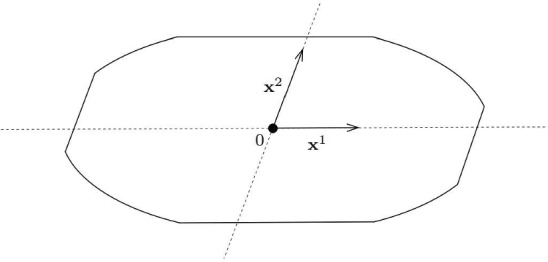
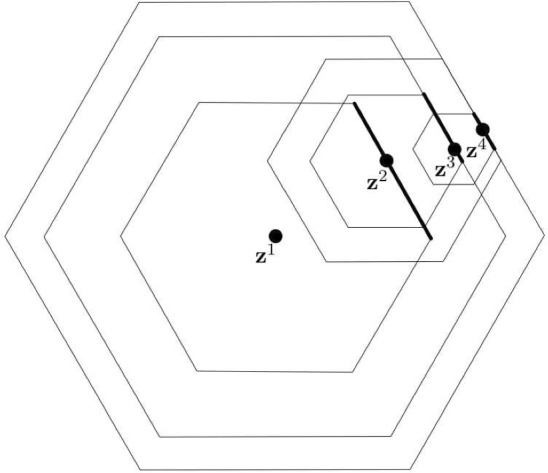
Monochromatic Infinite Sets in Minkowski Planes.

查看原文本刊更多论文

Monochromatic Infinite Sets in Minkowski Planes.

We prove that for any $ℓ_{p}$ -norm in the plane with $1 < p < \infty$ and for every infinite $M \subset R^{2}$ , there exists a two-colouring of the plane such that no isometric copy of $M$ is monochromatic. On the contrary, we show that for every polygonal norm (that is, the unit ball is a polygon) in the plane, there exists an infinite $M \subset R^{2}$ such that for every two-colouring of the plane there exists a monochromatic isometric copy of $M$ .

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Discrete & Computational Geometry 数学-计算机：理论方法

CiteScore

1.80

自引率

12.50%

发文量

审稿时长

6-12 weeks

期刊介绍： Discrete & Computational Geometry (DCG) is an international journal of mathematics and computer science, covering a broad range of topics in which geometry plays a fundamental role. It publishes papers on such topics as configurations and arrangements, spatial subdivision, packing, covering, and tiling, geometric complexity, polytopes, point location, geometric probability, geometric range searching, combinatorial and computational topology, probabilistic techniques in computational geometry, geometric graphs, geometry of numbers, and motion planning.