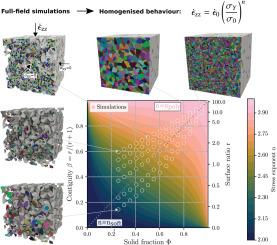
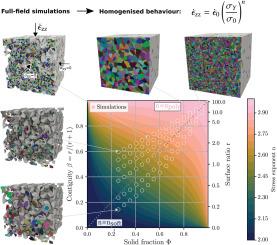
Sensitivity of the viscoplasticity of polycrystals to porosity and pore-to-crystal size ratio

Porous polycrystals are composed of pores and sintered crystals. Understanding their viscoplastic behaviour is crucial for predicting the mechanical performance of manufactured materials or the evolution of geological components. Their viscoplasticity intuitively depends on the shape of the solid matrix and how it is divided into individual crystals. Previous studies have primarily focused on limiting cases with low porosities or extreme pore-to-crystal size ratios. In this study, we use numerical full-field simulations on three-dimensional porous microstructures, combined with a crystal plasticity model, to explore how polycrystal viscoplasticity is affected by both geometric and crystalline structures. We use ice and its porous form, snow, as model materials. Our findings demonstrate that the homogenised strain rate $\dot{ϵ}$ fits a power law of stress $\sigma$ as $\dot{ϵ}={\left(\frac{\sigma }{{\sigma }_0}\right)}^n$ s⁻¹ with ${\sigma }_0$ the reference stress and $n$ the stress exponent. Notably, we show that the reference stress is determined solely by the geometric structure, while the stress exponent is influenced by both the geometric and crystalline structures. Specifically, the stress exponent is governed by the geometric frustration of the crystals caused by their neighbours, which modulates dislocation creep across different slip systems. By defining the pore-to-crystal size ratio as the area ratio between the crystal boundary and the free surface, we provide a coherent framework for understanding these interactions. This study clarifies the transitions in viscoplastic behaviour with varying porosity, avoiding the need for additional mechanisms and offering valuable insights into porous polycrystal viscoplasticity.