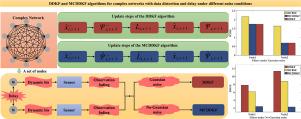
State estimation for time-varying complex networks with Gaussian and non-Gaussian noise: Addressing data distortion and delay

This paper investigates, for the first time, the state estimation (SE) problem in complex networks with data distortion and delay under various noise conditions. To address data distortion and delay effects caused by dynamic bias, observation fading, and random interference, this paper proposes two recursive state estimation algorithms based on Gaussian and non-Gaussian noise assumptions, respectively. Dynamic bias and observation fading are modeled using dynamic equations and a set of independent random variables, leading to the development of a new network system model. In Gaussian noise environments, an optimal data distortion and delay Kalman filter (DDKF) is proposed by improving the SE equations and error covariance bounds of the traditional delay-compensated state estimation (DCBSE) algorithm, significantly enhancing the SE accuracy. For non-Gaussian noise environments, the maximum correntropy criterion (MCC) is employed to maximize the cost function, resulting in the development of the maximum correntropy data distortion and delay Kalman filter (MCDDKF), which further improves the estimation accuracy and robustness of the DDKF under non-Gaussian noise conditions. Simulation results validate the effectiveness and applicability of both algorithms under different noise conditions.