边界上具有次线性非线性的logistic方程正解的边界层轮廓
IF 0.5
4区 数学
Q3 MATHEMATICS
引用次数: 0
摘要
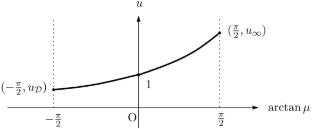
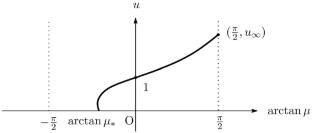
本文考虑logistic椭圆方程 \(-\Delta u = u- u^{p}\) 在光滑有界区域中 \(\Omega \subset {\mathbb {R}}^{N},\) \(N\ge 2,\) 具有次线性诺伊曼边界条件 \(\frac{\partial u}{\partial \nu } = \mu u^{q}\) on \(\partial \Omega ,\) 在哪里 \(0<q<1<p,\) 和 \(\mu \ge 0\) 是参数。利用该方程的子解和超解以及比较原理,我们分析了该方程的唯一正解的渐近轮廓 \(\mu \rightarrow \infty .\)本文章由计算机程序翻译,如有差异,请以英文原文为准。
Boundary layer profiles of positive solutions for logistic equations with sublinear nonlinearity on the boundary
In this paper, we consider the logistic elliptic equation \(-\Delta u = u- u^{p}\) in a smooth bounded domain \(\Omega \subset {\mathbb {R}}^{N},\) \(N\ge 2,\) equipped with the sublinear Neumann boundary condition \(\frac{\partial u}{\partial \nu } = \mu u^{q}\) on \(\partial \Omega ,\) where \(0<q<1<p,\) and \(\mu \ge 0\) is a parameter. With sub- and supersolutions and a comparison principle for the equation, we analyze the asymptotic profile of the unique positive solution for the equation as \(\mu \rightarrow \infty .\)
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊

Archiv der Mathematik
数学-数学
CiteScore
1.10
自引率
0.00%
发文量
117
审稿时长
4-8 weeks
期刊介绍:
Archiv der Mathematik (AdM) publishes short high quality research papers in every area of mathematics which are not overly technical in nature and addressed to a broad readership.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


