伯格流体中的热对流

Q2 Mathematics

Annali dell''Universita di Ferrara Pub Date : 2025-09-08 DOI:10.1007/s11565-025-00609-w

Brian Straughan

{"title":"伯格流体中的热对流","authors":"Brian Straughan","doi":"10.1007/s11565-025-00609-w","DOIUrl":null,"url":null,"abstract":"<div><p>The problem of thermal convection in a Burgers fluid occupying a horizontal layer is investigated. The thresholds for linear instability are calculated in detail and the critical Rayleigh and wave numbers are determined. Using a classification of Anatoly P. Oskolkov it is shown that the model for a Burgers fluid is a natural extension of a Maxwell fluid and one may also refer to it as a Maxwell fluid of order two. The thermal convection thresholds are compared to those for a regular Maxwell fluid and the effects of the new parameters in the Burgers model are displayed.</p></div>","PeriodicalId":35009,"journal":{"name":"Annali dell''Universita di Ferrara","volume":"71 4","pages":""},"PeriodicalIF":0.0000,"publicationDate":"2025-09-08","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"","citationCount":"0","resultStr":"{\"title\":\"Thermal convection in a Burgers fluid\",\"authors\":\"Brian Straughan\",\"doi\":\"10.1007/s11565-025-00609-w\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"<div><p>The problem of thermal convection in a Burgers fluid occupying a horizontal layer is investigated. The thresholds for linear instability are calculated in detail and the critical Rayleigh and wave numbers are determined. Using a classification of Anatoly P. Oskolkov it is shown that the model for a Burgers fluid is a natural extension of a Maxwell fluid and one may also refer to it as a Maxwell fluid of order two. The thermal convection thresholds are compared to those for a regular Maxwell fluid and the effects of the new parameters in the Burgers model are displayed.</p></div>\",\"PeriodicalId\":35009,\"journal\":{\"name\":\"Annali dell''Universita di Ferrara\",\"volume\":\"71 4\",\"pages\":\"\"},\"PeriodicalIF\":0.0000,\"publicationDate\":\"2025-09-08\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"\",\"citationCount\":\"0\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Annali dell''Universita di Ferrara\",\"FirstCategoryId\":\"1085\",\"ListUrlMain\":\"https://link.springer.com/article/10.1007/s11565-025-00609-w\",\"RegionNum\":0,\"RegionCategory\":null,\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"\",\"PubModel\":\"\",\"JCR\":\"Q2\",\"JCRName\":\"Mathematics\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Annali dell''Universita di Ferrara","FirstCategoryId":"1085","ListUrlMain":"https://link.springer.com/article/10.1007/s11565-025-00609-w","RegionNum":0,"RegionCategory":null,"ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q2","JCRName":"Mathematics","Score":null,"Total":0}

引用次数: 0

摘要

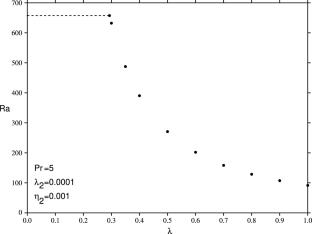
研究了占据水平层的Burgers流体中的热对流问题。详细计算了线性失稳的阈值，确定了临界瑞利数和波数。利用Anatoly P. Oskolkov的分类表明，Burgers流体模型是麦克斯韦流体的自然延伸，人们也可以将其称为二阶麦克斯韦流体。将热对流阈值与常规麦克斯韦流体的阈值进行了比较，并显示了Burgers模型中新参数的影响。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

Thermal convection in a Burgers fluid

查看原文本刊更多论文

Thermal convection in a Burgers fluid

The problem of thermal convection in a Burgers fluid occupying a horizontal layer is investigated. The thresholds for linear instability are calculated in detail and the critical Rayleigh and wave numbers are determined. Using a classification of Anatoly P. Oskolkov it is shown that the model for a Burgers fluid is a natural extension of a Maxwell fluid and one may also refer to it as a Maxwell fluid of order two. The thermal convection thresholds are compared to those for a regular Maxwell fluid and the effects of the new parameters in the Burgers model are displayed.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Annali dell''Universita di Ferrara Mathematics-Mathematics (all)

CiteScore

1.70

自引率

0.00%

发文量

期刊介绍： Annali dell''Università di Ferrara is a general mathematical journal publishing high quality papers in all aspects of pure and applied mathematics. After a quick preliminary examination, potentially acceptable contributions will be judged by appropriate international referees. Original research papers are preferred, but well-written surveys on important subjects are also welcome.