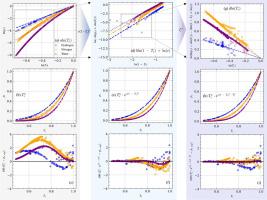
A new vapor pressure equation with accurate extrapolation capabilities

The vapor pressure equation is an effective tool for describing the pressure-temperature relationship along the liquid-vapor coexistence curve. However, most existing equations are merely used to correlate experimental data, but lack reliability when extrapolating beyond the experimental temperature range. Based on the thermodynamic characteristics of vapor pressure, this study summarizes the mathematical constraints of vapor pressure equation, and proposes a new, accurate and reliable vapor pressure equation with four fitting parameters for the correlation and extrapolation of experimental data. The new equation is compared with the Park equation and Wagner equation in terms of correlation and extrapolation performance using experimental data of 62 fluids from the triple point to the critical point. Results show that the new equation matches or slightly outperforms the Park equation and Wagner equation in correlation accuracy, while it has more regular fitting parameters. In terms of extrapolation, the new equation significantly outperforms the Park equation and Wagner equation without parameter constraints, especially towards low-temperature and low-pressure region. And the new equation presents stable extrapolation across different data ranges, achieving a balance between correlation accuracy and extrapolation ability through rigorously validated function forms and reasonably set fitting parameters.