凸包络法的T,p闪速计算具有任意数量的组分和任意聚合状态的混合物
IF 3.9
2区 工程技术
Q2 COMPUTER SCIENCE, INTERDISCIPLINARY APPLICATIONS
引用次数: 0
摘要
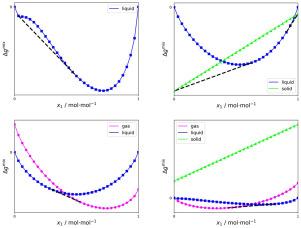
T,p闪蒸计算确定相平衡时的正确相数及其在固定温度和压力下的组成。它们对于化工过程的模拟和优化是必不可少的。凸包络法(CEM)是一种利用切平面判据来确定任意组分混合物的液相平衡而不预先提供相数的方法。这项工作将CEM扩展到包括气相和固相。因此,具有任意数量的组分和相的给定混合物的任何相平衡都可以在整个组成空间上计算。CEM结果给出了各种气-液和固-液相平衡的例子,最多四个组分。我们展示了CEM如何用于ge模型的参数拟合。展望未来,我们展示了如何将CEM与基于机器学习的属性预测工具相结合,以构建相平衡。本文章由计算机程序翻译,如有差异,请以英文原文为准。
Convex envelope method for T,p flash calculations for mixtures with an arbitrary number of components and arbitrary aggregate states
flash calculations determine the correct number of phases at phase equilibrium and their compositions for fixed temperature and pressure. They are essential for chemical process simulation and optimization. The convex envelope method (CEM) is an existing approach that employs the tangent plane criterion to determine liquid phase equilibria for mixtures with an arbitrary number of components without providing the number of phases beforehand. This work extends the CEM to include also vapor and solid phases. Thus, any phase equilibrium of a given mixture with an arbitrary number of components and phases can be calculated over the whole composition space. The CEM results are presented for various vapor–liquid and solid–liquid phase equilibria examples of up to four components. We show how the CEM can be used for parameter fitting of -models. As an outlook, we demonstrate how the CEM can be combined with a machine learning-based tool for property prediction to construct phase equilibria.
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊

Computers & Chemical Engineering
工程技术-工程:化工
CiteScore
8.70
自引率
14.00%
发文量
374
审稿时长
70 days
期刊介绍:
Computers & Chemical Engineering is primarily a journal of record for new developments in the application of computing and systems technology to chemical engineering problems.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


