利用信息论理解自编码器在刚性动力系统中的作用
IF 9.6
Q1 COMPUTER SCIENCE, ARTIFICIAL INTELLIGENCE
引用次数: 0
摘要
本文运用信息论的方法,探讨了利用深度神经网络(DNN)训练构建自编码器(AE)的潜在空间如何在刚性动力系统中找到光滑(非刚性)低维流形。我们最近的研究(Vijayarangan et al. 2023)报道,将AE与神经ODE (NODE)相结合作为替代降阶模型(ROM),用于整合刚性化学反应系统,导致时间刚度显著降低,这种行为归因于使用AE通过非线性投影识别慢不变流形。本研究通过运用信息论和更好的混合概念,对非刚性潜空间的形成机制和刚度降低提供了一个基本的理解。编码器和解码器的学习机制是通过绘制互信息的演变和识别两个不同的阶段来解释的。随后,绘制了物理变量和潜变量的密度分布,显示了由非线性自编码器提供的物理空间中的罕见事件向潜空间中的高可能(更可能)事件的转换。最后,利用信息论和概率论的概念解释了导致密度重分布的非线性变换。本文章由计算机程序翻译,如有差异,请以英文原文为准。
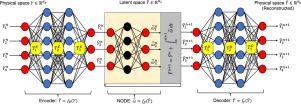
Understanding the role of autoencoders for stiff dynamical systems using information theory
Using information theory, this study provides insights into how the construction of latent space of autoencoder (AE) using deep neural network (DNN) training finds a smooth (non-stiff) low-dimensional manifold in the stiff dynamical system. Our recent study (Vijayarangan et al. 2023) reported that an AE combined with neural ODE (NODE) as a surrogate reduced order model (ROM) for the integration of stiff chemically reacting systems led to a significant reduction in the temporal stiffness, and the behavior was attributed to the identification of a slow invariant manifold by the nonlinear projection using the AE. The present work offers a fundamental understanding of the mechanism of formation of a non-stiff latent space and stiffness reduction by employing concepts from information theory and better mixing. The learning mechanisms of both the encoder and the decoder are explained by plotting the evolution of mutual information and identifying two different phases. Subsequently, the density distribution is plotted for the physical and latent variables, which shows the transformation of the rare event in the physical space to a highly likely (more probable) event in the latent space provided by the nonlinear autoencoder. Finally, the nonlinear transformation leading to density redistribution is explained using concepts from information theory and probability.
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊

Energy and AI
Engineering-Engineering (miscellaneous)
CiteScore
16.50
自引率
0.00%
发文量
64
审稿时长
56 days
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


