使用收缩方法解决年龄依赖性传染病和肿瘤生长模型
IF 1.9
Q2 MULTIDISCIPLINARY SCIENCES
引用次数: 0
摘要
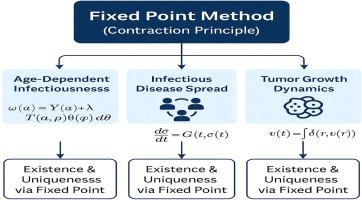
本文建立了年龄依赖性疾病传染性、传染病传播和肿瘤生长动力学三个生物建模领域解集的存在性和唯一性定理。我们说明不动点理论,利用收缩映射概念,为模型稳定性和解一致性提供了坚实的数学基础。我们的主要贡献是发展广义收缩技术,以确保描述这些生物系统的微分方程解的存在性和唯一性。这个数学框架提高了流行病学和肿瘤学建模的数学熟练程度,并为模型验证提供了计算技术。这些发现通过采用经典分析中的定点方法来管理生物系统中存在的复杂非线性,从而解决了科学文献中的重大缺陷,从而为疾病动力学和治疗效果的研究铺平了新的道路。•目的:在这项工作中,我们将在肿瘤生长、传染病依赖和传播等模型中寻找方程唯一解的存在准则。•方法:利用收缩原理,利用文献中的不同收缩,如f收缩,α- f收缩,有理型(ψ, φ)收缩和geraghty型收缩,我们提出了上述生物模型具有唯一解的条件。•发现:在不同的条件下,我们建立了新的结果,通过分析上述生物模型中出现的问题解决方案的存在性和唯一性,帮助我们确保了稳定性。本文章由计算机程序翻译,如有差异,请以英文原文为准。
Solving age-dependent infectious diseases and tumor growth models using the contraction approach
This study establishes existence and uniqueness theorems for solution sets in three domains of biological modeling: age-dependent diseases infectiousness, infectious disease transmission, and tumor growth dynamics. We illustrate that fixed-point theory, using contraction mapping concepts, offers solid mathematical foundations for model stability and solution consistency. Our principal contribution is to develop generalized contraction techniques that ensure the existence and uniqueness of solutions for the differential equations describing these biological systems. This mathematical framework improves the mathematical proficiency of epidemiological and oncological modeling and offers computational techniques for model validation. These findings address significant deficiencies in the scientific literature by employing fixed-point methodologies from classical analysis to manage the intricate nonlinearities present in biological systems, thereby paving emerging paths for the investigation of disease dynamics and treatment effectiveness.
- •Purpose: In this work, we will look for the criteria of existence of unique solutions of the equations in the models like, tumor growth, infectious diseases dependency and spread.
- •Methodology: Utilizing contraction principle and using different contractions from the literature like, F-contraction, α-F-contraction, rational type (ψ, φ)-contraction, and Geraghty-type contraction we come up with the conditions where the mentioned biological models possesses unique solutions.
- •Findings: Imposing different conditions we established novel results which help us ensure the stability by analyzing the existence and uniqueness of the solution of the problems arising in the aforementioned biological models.
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊

MethodsX
Health Professions-Medical Laboratory Technology
CiteScore
3.60
自引率
5.30%
发文量
314
审稿时长
7 weeks
期刊介绍:
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


