有限强度源稳定辐射波的指数渐近处理
IF 2.9
3区 数学
Q1 MATHEMATICS, APPLIED
引用次数: 0
摘要
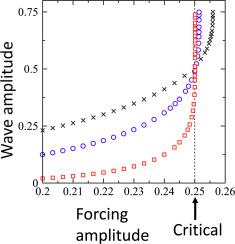
我们重新考察了稳定强迫Korteweg-deVries (fKdV)方程,该方程具有光滑的局部受限强迫项和远上游无波的辐射条件。当色散较小(μ≪1)时,在计算下游的辐射波时,即使波幅相对于μ呈指数级小,也不能忽视非线性。早先的研究在强迫项强度控制的非线性较弱且与色散相平衡的假设下,通过指数渐近法在极限μ→0处计算了该波。在这里,我们开发了一个单独的指数渐近理论,辐射波由于0(1)强度的强迫。与以往工作的根本区别在于,波幅的指数小因子的指数是由强迫振幅A控制的,强迫振幅A由上面的某个临界值Acrit=O(1)限定。此外,当A接近Acrit时,该指数趋于零。因此,本理论弥补了先前计算出的A≪1的指数级小波与A靠近Acrit时产生的陡波(余弦波)之间的差距。fKdV方程的直接数值解支持了渐近结果。此外,数值结果证实了Acrit是一个极限强迫幅值,超过此值,稳定解向下游发散。本文章由计算机程序翻译,如有差异,请以英文原文为准。
Exponential-asymptotics treatment of steady radiating waves from sources of finite strength
We re-visit the steady forced Korteweg–deVries (fKdV) equation with a smooth locally confined forcing term and the radiation condition of no waves far upstream. When dispersion is small (), nonlinearity cannot be ignored in computing the radiating wave downstream even though the wave amplitude is exponentially small relative to . Earlier studies computed this wave in the limit via exponential asymptotics, on the assumption that nonlinearity, which is controlled by the strength of the forcing term, is weak and balances with dispersion. Here, we develop a separate exponential asymptotics theory for radiating waves due to forcing of strength. A fundamental difference from previous work is that the exponent of the exponentially small factor of the wave amplitude is controlled by the forcing amplitude , which is bound from above by a certain critical value . Furthermore, this exponent tends to zero as approaches . Thus, the present theory bridges the gap between the exponentially small waves computed earlier for and the steep (cnoidal) waves that arise when is near . The asymptotic results are supported by direct numerical solutions of the fKdV equation. Furthermore, the numerical results confirm that is a limiting forcing amplitude, beyond which steady solutions diverge downstream.
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊

Physica D: Nonlinear Phenomena
物理-物理:数学物理
CiteScore
7.30
自引率
7.50%
发文量
213
审稿时长
65 days
期刊介绍:
Physica D (Nonlinear Phenomena) publishes research and review articles reporting on experimental and theoretical works, techniques and ideas that advance the understanding of nonlinear phenomena. Topics encompass wave motion in physical, chemical and biological systems; physical or biological phenomena governed by nonlinear field equations, including hydrodynamics and turbulence; pattern formation and cooperative phenomena; instability, bifurcations, chaos, and space-time disorder; integrable/Hamiltonian systems; asymptotic analysis and, more generally, mathematical methods for nonlinear systems.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


