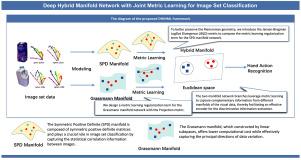
Deep Hybrid Manifold Network with joint metric learning for image set classification

Many studies have shown that complex visual data exhibit non-linear and non-Euclidean characteristics. How to find an intrinsic and low-dimensional representation for non-linear visual data is crucial for image set classification. Due to the powerful data interpretation of deep neural networks and the intrinsic structural exploitation of manifold learning, deep Riemannian neural networks have demonstrated excellent performance on solving the non-linear and non-Euclidean data. However, on the one hand, deep Riemannian neural networks usually focus on exploring the intrinsic structure of the single manifold, while complex visual data may contain multiple potential intrinsic structures. On the other hand, the single cross-entropy is usually adopted as the sole loss function, which may lose discriminative metric information. In this paper, we propose a deep Riemannian neural network by fusing Symmetric Positive Definite (SPD) and Grassmann manifolds to explore multiple intrinsic structures in complex visual data. We innovatively employ the Jensen–Bregman LogDet Divergence and Projection metric to construct two metric learning regularization terms over SPD and Grassmann manifold networks respectively, which capture the intra-class and inter-class data distributions. Subsequently, the regularization terms corresponding to different manifolds are jointly learned in conjunction with the cross-entropy loss function to fuse multiple loss information. Extensive experiments are conducted on expression recognition, gesture recognition, and action recognition tasks. Experimental results demonstrate the superior performance of the proposed Riemannian network.