2列表对应的量子仿射代数素模的分类。

IF 0.9 3区数学 Q3 MATHEMATICS

Journal of Algebraic Combinatorics Pub Date : 2025-01-01 Epub Date: 2025-07-15 DOI:10.1007/s10801-025-01435-1

Nick Early, Jian-Rong Li

{"title":"2列表对应的量子仿射代数素模的分类。","authors":"Nick Early, Jian-Rong Li","doi":"10.1007/s10801-025-01435-1","DOIUrl":null,"url":null,"abstract":"Finite-dimensional simple modules of quantum affine algebras of type A correspond to semistandard Young tableaux of rectangular shapes. In this paper, we classify all prime modules corresponding to 2-column semistandard Young tableaux, up to a conjectural property. Moreover, we give a conjectural sufficient condition for a module corresponding to a tableau with more than two columns to be prime.","PeriodicalId":14926,"journal":{"name":"Journal of Algebraic Combinatorics","volume":"62 1","pages":"6"},"PeriodicalIF":0.9000,"publicationDate":"2025-01-01","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"https://www.ncbi.nlm.nih.gov/pmc/articles/PMC12263800/pdf/","citationCount":"0","resultStr":"{\"title\":\"Classification of prime modules of quantum affine algebras corresponding to 2-column tableaux.\",\"authors\":\"Nick Early, Jian-Rong Li\",\"doi\":\"10.1007/s10801-025-01435-1\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"Finite-dimensional simple modules of quantum affine algebras of type A correspond to semistandard Young tableaux of rectangular shapes. In this paper, we classify all prime modules corresponding to 2-column semistandard Young tableaux, up to a conjectural property. Moreover, we give a conjectural sufficient condition for a module corresponding to a tableau with more than two columns to be prime.\",\"PeriodicalId\":14926,\"journal\":{\"name\":\"Journal of Algebraic Combinatorics\",\"volume\":\"62 1\",\"pages\":\"6\"},\"PeriodicalIF\":0.9000,\"publicationDate\":\"2025-01-01\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"https://www.ncbi.nlm.nih.gov/pmc/articles/PMC12263800/pdf/\",\"citationCount\":\"0\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Journal of Algebraic Combinatorics\",\"FirstCategoryId\":\"100\",\"ListUrlMain\":\"https://doi.org/10.1007/s10801-025-01435-1\",\"RegionNum\":3,\"RegionCategory\":\"数学\",\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"2025/7/15 0:00:00\",\"PubModel\":\"Epub\",\"JCR\":\"Q3\",\"JCRName\":\"MATHEMATICS\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Journal of Algebraic Combinatorics","FirstCategoryId":"100","ListUrlMain":"https://doi.org/10.1007/s10801-025-01435-1","RegionNum":3,"RegionCategory":"数学","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"2025/7/15 0:00:00","PubModel":"Epub","JCR":"Q3","JCRName":"MATHEMATICS","Score":null,"Total":0}

引用次数: 0

摘要

A型量子仿射代数的有限维简单模对应于矩形形状的半标准杨氏表。本文对2列半标准杨表所对应的素模进行了分类，直到一个猜想性质为止。此外，我们还给出了两列以上表所对应的模为素数的一个推测性充分条件。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

查看原文本刊更多论文

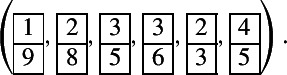
Classification of prime modules of quantum affine algebras corresponding to 2-column tableaux.

Finite-dimensional simple modules of quantum affine algebras of type A correspond to semistandard Young tableaux of rectangular shapes. In this paper, we classify all prime modules corresponding to 2-column semistandard Young tableaux, up to a conjectural property. Moreover, we give a conjectural sufficient condition for a module corresponding to a tableau with more than two columns to be prime.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Journal of Algebraic Combinatorics 数学-数学

CiteScore

1.50

自引率

12.50%

发文量

审稿时长

6-12 weeks

期刊介绍： The Journal of Algebraic Combinatorics provides a single forum for papers on algebraic combinatorics which, at present, are distributed throughout a number of journals. Within the last decade or so, algebraic combinatorics has evolved into a mature, established and identifiable area of mathematics. Research contributions in the field are increasingly seen to have substantial links with other areas of mathematics. The journal publishes papers in which combinatorics and algebra interact in a significant and interesting fashion. This interaction might occur through the study of combinatorial structures using algebraic methods, or the application of combinatorial methods to algebraic problems.