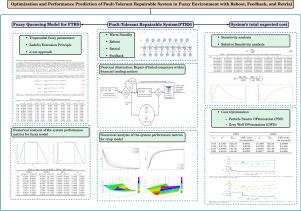
Optimization and performance prediction of fault-tolerant repairable system in fuzzy environment with reboot, feedback, and retrial

This study investigates stochastic modeling of a repairable redundant fault-tolerant system with feedback policy, standby support, retrial, and reboot features. The steady-state queue size distributions are derived using a recursive approach. The queueing model is transformed from a crisp to a fuzzy environment through Zadeh’s extension principle and $\alpha$-cut approach. Numerical simulations are conducted to analyze the system performance metrics with respect to diverse system parameters. The total expected cost of the fault-tolerant repairable system is established. Followed by sensitivity analysis and relative sensitivity analysis, we evaluate the system indices and their behavior corresponding to the system parameters. Furthermore, the cost is optimized using meta-heuristic approaches, namely Grey Wolf Optimization (GWO) and Particle Swarm Optimization (PSO). A practical illustration demonstrating the applicability of the proposed model, with a focus on the high-frequency trading systems in financial markets, is provided.