变形Wigner矩阵的预热化。

IF 1.3 3区物理与天体物理 Q2 PHYSICS, MATHEMATICAL

Annales Henri Poincaré Pub Date : 2024-12-17 DOI:10.1007/s00023-024-01518-y

László Erdős, Joscha Henheik, Jana Reker, Volodymyr Riabov

{"title":"变形Wigner矩阵的预热化。","authors":"László Erdős, Joscha Henheik, Jana Reker, Volodymyr Riabov","doi":"10.1007/s00023-024-01518-y","DOIUrl":null,"url":null,"abstract":"<div>We prove that a class of weakly perturbed Hamiltonians of the form \\(H_\\lambda = H_0 + \\lambda W\\), with W being a Wigner matrix, exhibits prethermalization. That is, the time evolution generated by \\(H_\\lambda \\) relaxes to its ultimate thermal state via an intermediate prethermal state with a lifetime of order \\(\\lambda ^{-2}\\). Moreover, we obtain a general relaxation formula, expressing the perturbed dynamics via the unperturbed dynamics and the ultimate thermal state. The proof relies on a two-resolvent law for the deformed Wigner matrix \\(H_\\lambda \\).</div>","PeriodicalId":463,"journal":{"name":"Annales Henri Poincaré","volume":"26 6","pages":"1991 - 2033"},"PeriodicalIF":1.3000,"publicationDate":"2024-12-17","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"https://www.ncbi.nlm.nih.gov/pmc/articles/PMC12133972/pdf/","citationCount":"0","resultStr":"{\"title\":\"Prethermalization for Deformed Wigner Matrices\",\"authors\":\"László Erdős, Joscha Henheik, Jana Reker, Volodymyr Riabov\",\"doi\":\"10.1007/s00023-024-01518-y\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"<div>We prove that a class of weakly perturbed Hamiltonians of the form \\\\(H_\\\\lambda = H_0 + \\\\lambda W\\\\), with W being a Wigner matrix, exhibits prethermalization. That is, the time evolution generated by \\\\(H_\\\\lambda \\\\) relaxes to its ultimate thermal state via an intermediate prethermal state with a lifetime of order \\\\(\\\\lambda ^{-2}\\\\). Moreover, we obtain a general relaxation formula, expressing the perturbed dynamics via the unperturbed dynamics and the ultimate thermal state. The proof relies on a two-resolvent law for the deformed Wigner matrix \\\\(H_\\\\lambda \\\\).</div>\",\"PeriodicalId\":463,\"journal\":{\"name\":\"Annales Henri Poincaré\",\"volume\":\"26 6\",\"pages\":\"1991 - 2033\"},\"PeriodicalIF\":1.3000,\"publicationDate\":\"2024-12-17\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"https://www.ncbi.nlm.nih.gov/pmc/articles/PMC12133972/pdf/\",\"citationCount\":\"0\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Annales Henri Poincaré\",\"FirstCategoryId\":\"4\",\"ListUrlMain\":\"https://link.springer.com/article/10.1007/s00023-024-01518-y\",\"RegionNum\":3,\"RegionCategory\":\"物理与天体物理\",\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"\",\"PubModel\":\"\",\"JCR\":\"Q2\",\"JCRName\":\"PHYSICS, MATHEMATICAL\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Annales Henri Poincaré","FirstCategoryId":"4","ListUrlMain":"https://link.springer.com/article/10.1007/s00023-024-01518-y","RegionNum":3,"RegionCategory":"物理与天体物理","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q2","JCRName":"PHYSICS, MATHEMATICAL","Score":null,"Total":0}

引用次数: 0

摘要

证明了一类弱摄动哈密顿量H λ = H 0 + λ W，其中W为Wigner矩阵，表现出预热化。也就是说，H λ产生的时间演化通过一个寿命为λ - 2阶的中间预热状态松弛到其最终热态。此外，我们还得到了一个通用的松弛公式，通过无扰动动力学和极限热态来表示扰动动力学。该证明依赖于变形Wigner矩阵H λ的双解律。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

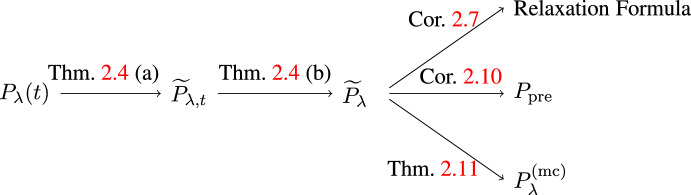
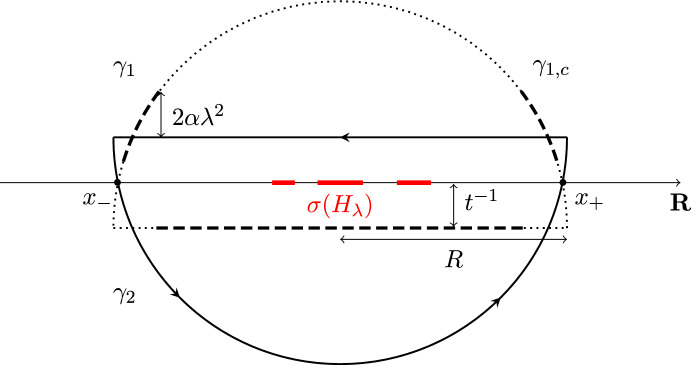
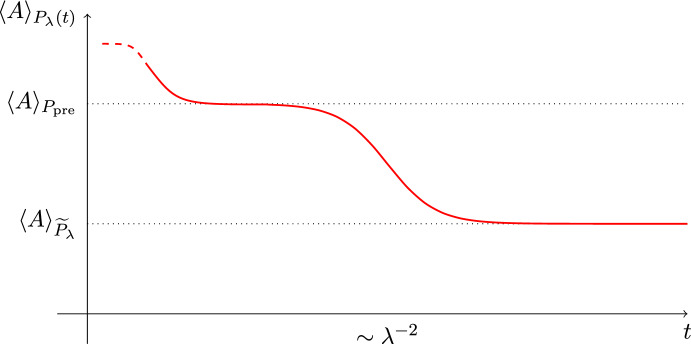
Prethermalization for Deformed Wigner Matrices

查看原文本刊更多论文

Prethermalization for Deformed Wigner Matrices

We prove that a class of weakly perturbed Hamiltonians of the form \(H_\lambda = H_0 + \lambda W\), with W being a Wigner matrix, exhibits prethermalization. That is, the time evolution generated by \(H_\lambda \) relaxes to its ultimate thermal state via an intermediate prethermal state with a lifetime of order \(\lambda ^{-2}\). Moreover, we obtain a general relaxation formula, expressing the perturbed dynamics via the unperturbed dynamics and the ultimate thermal state. The proof relies on a two-resolvent law for the deformed Wigner matrix \(H_\lambda \).

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Annales Henri Poincaré 物理-物理：粒子与场物理

CiteScore

3.00

自引率

6.70%

发文量

108

审稿时长

6-12 weeks

期刊介绍： The two journals Annales de l''Institut Henri Poincaré, physique théorique and Helvetica Physical Acta merged into a single new journal under the name Annales Henri Poincaré - A Journal of Theoretical and Mathematical Physics edited jointly by the Institut Henri Poincaré and by the Swiss Physical Society. The goal of the journal is to serve the international scientific community in theoretical and mathematical physics by collecting and publishing original research papers meeting the highest professional standards in the field. The emphasis will be on analytical theoretical and mathematical physics in a broad sense.