化学反应型和磁铁矿型Cu-Al2O3水基混合纳米流体在Riga板上的热扩散和质量扩散特性的数值研究
IF 2.9
4区 工程技术
Q1 MULTIDISCIPLINARY SCIENCES
Govind, Pooja Sharma, Ravi Chaudhary, B. K. Sharma, Preeti, Faisal Z. Duraihem
{"title":"化学反应型和磁铁矿型Cu-Al2O3水基混合纳米流体在Riga板上的热扩散和质量扩散特性的数值研究","authors":"Govind, Pooja Sharma, Ravi Chaudhary, B. K. Sharma, Preeti, Faisal Z. Duraihem","doi":"10.1002/adts.202500352","DOIUrl":null,"url":null,"abstract":"The existing work intends to explore the thermal and mass diffusion properties in chemically reactive and magnetite hybrid nanofluids (consisting of <span data-altimg=\"/cms/asset/f0a514a9-3c88-4a53-bc8c-1ca644cdaa33/adts70009-math-0001.png\"></span><mjx-container ctxtmenu_counter=\"10\" ctxtmenu_oldtabindex=\"1\" jax=\"CHTML\" role=\"application\" sre-explorer- style=\"font-size: 103%; position: relative;\" tabindex=\"0\"><mjx-math aria-hidden=\"true\" location=\"graphic/adts70009-math-0001.png\"><mjx-semantics><mjx-mrow><mjx-mrow data-semantic-children=\"12,8\" data-semantic-content=\"7\" data-semantic- data-semantic-role=\"division\" data-semantic-speech=\"normal upper A normal l 2 normal upper O 3 divided by upper C u\" data-semantic-type=\"infixop\"><mjx-mrow data-semantic-annotation=\"clearspeak:unit\" data-semantic-children=\"0,3,6\" data-semantic-content=\"10,11\" data-semantic- data-semantic-parent=\"13\" data-semantic-role=\"implicit\" data-semantic-type=\"infixop\"><mjx-mi data-semantic-annotation=\"clearspeak:simple\" data-semantic-font=\"normal\" data-semantic- data-semantic-parent=\"12\" data-semantic-role=\"latinletter\" data-semantic-type=\"identifier\"><mjx-c></mjx-c></mjx-mi><mjx-mo data-semantic-added=\"true\" data-semantic- data-semantic-operator=\"infixop,\" data-semantic-parent=\"12\" data-semantic-role=\"multiplication\" data-semantic-type=\"operator\" style=\"margin-left: 0.056em; margin-right: 0.056em;\"><mjx-c></mjx-c></mjx-mo><mjx-msub data-semantic-children=\"1,2\" data-semantic- data-semantic-parent=\"12\" data-semantic-role=\"latinletter\" data-semantic-type=\"subscript\"><mjx-mi data-semantic-annotation=\"clearspeak:simple\" data-semantic-font=\"normal\" data-semantic- data-semantic-parent=\"3\" data-semantic-role=\"latinletter\" data-semantic-type=\"identifier\"><mjx-c></mjx-c></mjx-mi><mjx-script style=\"vertical-align: -0.15em;\"><mjx-mn data-semantic-annotation=\"clearspeak:simple\" data-semantic-font=\"normal\" data-semantic- data-semantic-parent=\"3\" data-semantic-role=\"integer\" data-semantic-type=\"number\" size=\"s\"><mjx-c></mjx-c></mjx-mn></mjx-script></mjx-msub><mjx-mo data-semantic-added=\"true\" data-semantic- data-semantic-operator=\"infixop,\" data-semantic-parent=\"12\" data-semantic-role=\"multiplication\" data-semantic-type=\"operator\" style=\"margin-left: 0.056em; margin-right: 0.056em;\"><mjx-c></mjx-c></mjx-mo><mjx-msub data-semantic-children=\"4,5\" data-semantic- data-semantic-parent=\"12\" data-semantic-role=\"latinletter\" data-semantic-type=\"subscript\"><mjx-mi data-semantic-annotation=\"clearspeak:simple\" data-semantic-font=\"normal\" data-semantic- data-semantic-parent=\"6\" data-semantic-role=\"latinletter\" data-semantic-type=\"identifier\"><mjx-c></mjx-c></mjx-mi><mjx-script style=\"vertical-align: -0.15em;\"><mjx-mn data-semantic-annotation=\"clearspeak:simple\" data-semantic-font=\"normal\" data-semantic- data-semantic-parent=\"6\" data-semantic-role=\"integer\" data-semantic-type=\"number\" size=\"s\"><mjx-c></mjx-c></mjx-mn></mjx-script></mjx-msub></mjx-mrow><mjx-mo data-semantic- data-semantic-operator=\"infixop,/\" data-semantic-parent=\"13\" data-semantic-role=\"division\" data-semantic-type=\"operator\" rspace=\"1\" space=\"1\"><mjx-c></mjx-c></mjx-mo><mjx-mi data-semantic-font=\"normal\" data-semantic- data-semantic-parent=\"13\" data-semantic-role=\"unknown\" data-semantic-type=\"identifier\"><mjx-c></mjx-c><mjx-c></mjx-c></mjx-mi></mjx-mrow><mjx-mspace style=\"width: 0.28em;\"></mjx-mspace></mjx-mrow></mjx-semantics></mjx-math><mjx-assistive-mml display=\"inline\" unselectable=\"on\"><math altimg=\"urn:x-wiley:25130390:media:adts70009:adts70009-math-0001\" display=\"inline\" location=\"graphic/adts70009-math-0001.png\" xmlns=\"http://www.w3.org/1998/Math/MathML\"><semantics><mrow><mrow data-semantic-=\"\" data-semantic-children=\"12,8\" data-semantic-content=\"7\" data-semantic-role=\"division\" data-semantic-speech=\"normal upper A normal l 2 normal upper O 3 divided by upper C u\" data-semantic-type=\"infixop\"><mrow data-semantic-=\"\" data-semantic-annotation=\"clearspeak:unit\" data-semantic-children=\"0,3,6\" data-semantic-content=\"10,11\" data-semantic-parent=\"13\" data-semantic-role=\"implicit\" data-semantic-type=\"infixop\"><mi data-semantic-=\"\" data-semantic-annotation=\"clearspeak:simple\" data-semantic-font=\"normal\" data-semantic-parent=\"12\" data-semantic-role=\"latinletter\" data-semantic-type=\"identifier\" mathvariant=\"normal\">A</mi><mo data-semantic-=\"\" data-semantic-added=\"true\" data-semantic-operator=\"infixop,\" data-semantic-parent=\"12\" data-semantic-role=\"multiplication\" data-semantic-type=\"operator\"></mo><msub data-semantic-=\"\" data-semantic-children=\"1,2\" data-semantic-parent=\"12\" data-semantic-role=\"latinletter\" data-semantic-type=\"subscript\"><mi data-semantic-=\"\" data-semantic-annotation=\"clearspeak:simple\" data-semantic-font=\"normal\" data-semantic-parent=\"3\" data-semantic-role=\"latinletter\" data-semantic-type=\"identifier\" mathvariant=\"normal\">l</mi><mn data-semantic-=\"\" data-semantic-annotation=\"clearspeak:simple\" data-semantic-font=\"normal\" data-semantic-parent=\"3\" data-semantic-role=\"integer\" data-semantic-type=\"number\">2</mn></msub><mo data-semantic-=\"\" data-semantic-added=\"true\" data-semantic-operator=\"infixop,\" data-semantic-parent=\"12\" data-semantic-role=\"multiplication\" data-semantic-type=\"operator\"></mo><msub data-semantic-=\"\" data-semantic-children=\"4,5\" data-semantic-parent=\"12\" data-semantic-role=\"latinletter\" data-semantic-type=\"subscript\"><mi data-semantic-=\"\" data-semantic-annotation=\"clearspeak:simple\" data-semantic-font=\"normal\" data-semantic-parent=\"6\" data-semantic-role=\"latinletter\" data-semantic-type=\"identifier\" mathvariant=\"normal\">O</mi><mn data-semantic-=\"\" data-semantic-annotation=\"clearspeak:simple\" data-semantic-font=\"normal\" data-semantic-parent=\"6\" data-semantic-role=\"integer\" data-semantic-type=\"number\">3</mn></msub></mrow><mo data-semantic-=\"\" data-semantic-operator=\"infixop,/\" data-semantic-parent=\"13\" data-semantic-role=\"division\" data-semantic-type=\"operator\">/</mo><mi data-semantic-=\"\" data-semantic-font=\"normal\" data-semantic-parent=\"13\" data-semantic-role=\"unknown\" data-semantic-type=\"identifier\">Cu</mi></mrow><mspace width=\"0.28em\"></mspace></mrow>${\\mathrm{A}}{{\\mathrm{l}}_{2 }}{{\\mathrm{O}}_3}/{\\mathrm{Cu}}\\;$</annotation></semantics></math></mjx-assistive-mml></mjx-container> nanoparticles dispersed in <span data-altimg=\"/cms/asset/437e1cb3-62db-4991-a939-035e4b38558d/adts70009-math-0002.png\"></span><mjx-container ctxtmenu_counter=\"11\" ctxtmenu_oldtabindex=\"1\" jax=\"CHTML\" role=\"application\" sre-explorer- style=\"font-size: 103%; position: relative;\" tabindex=\"0\"><mjx-math aria-hidden=\"true\" location=\"graphic/adts70009-math-0002.png\"><mjx-semantics><mjx-mrow data-semantic-annotation=\"clearspeak:unit\" data-semantic-children=\"2,3\" data-semantic-content=\"4\" data-semantic- data-semantic-role=\"implicit\" data-semantic-speech=\"normal upper H 2 normal upper O\" data-semantic-type=\"infixop\"><mjx-msub data-semantic-children=\"0,1\" data-semantic- data-semantic-parent=\"5\" data-semantic-role=\"latinletter\" data-semantic-type=\"subscript\"><mjx-mi data-semantic-annotation=\"clearspeak:simple\" data-semantic-font=\"normal\" data-semantic- data-semantic-parent=\"2\" data-semantic-role=\"latinletter\" data-semantic-type=\"identifier\"><mjx-c></mjx-c></mjx-mi><mjx-script style=\"vertical-align: -0.15em;\"><mjx-mn data-semantic-annotation=\"clearspeak:simple\" data-semantic-font=\"normal\" data-semantic- data-semantic-parent=\"2\" data-semantic-role=\"integer\" data-semantic-type=\"number\" size=\"s\"><mjx-c></mjx-c></mjx-mn></mjx-script></mjx-msub><mjx-mo data-semantic-added=\"true\" data-semantic- data-semantic-operator=\"infixop,\" data-semantic-parent=\"5\" data-semantic-role=\"multiplication\" data-semantic-type=\"operator\" style=\"margin-left: 0.056em; margin-right: 0.056em;\"><mjx-c></mjx-c></mjx-mo><mjx-mi data-semantic-annotation=\"clearspeak:simple\" data-semantic-font=\"normal\" data-semantic- data-semantic-parent=\"5\" data-semantic-role=\"latinletter\" data-semantic-type=\"identifier\"><mjx-c></mjx-c></mjx-mi></mjx-mrow></mjx-semantics></mjx-math><mjx-assistive-mml display=\"inline\" unselectable=\"on\"><math altimg=\"urn:x-wiley:25130390:media:adts70009:adts70009-math-0002\" display=\"inline\" location=\"graphic/adts70009-math-0002.png\" xmlns=\"http://www.w3.org/1998/Math/MathML\"><semantics><mrow data-semantic-=\"\" data-semantic-annotation=\"clearspeak:unit\" data-semantic-children=\"2,3\" data-semantic-content=\"4\" data-semantic-role=\"implicit\" data-semantic-speech=\"normal upper H 2 normal upper O\" data-semantic-type=\"infixop\"><msub data-semantic-=\"\" data-semantic-children=\"0,1\" data-semantic-parent=\"5\" data-semantic-role=\"latinletter\" data-semantic-type=\"subscript\"><mi data-semantic-=\"\" data-semantic-annotation=\"clearspeak:simple\" data-semantic-font=\"normal\" data-semantic-parent=\"2\" data-semantic-role=\"latinletter\" data-semantic-type=\"identifier\" mathvariant=\"normal\">H</mi><mn data-semantic-=\"\" data-semantic-annotation=\"clearspeak:simple\" data-semantic-font=\"normal\" data-semantic-parent=\"2\" data-semantic-role=\"integer\" data-semantic-type=\"number\">2</mn></msub><mo data-semantic-=\"\" data-semantic-added=\"true\" data-semantic-operator=\"infixop,\" data-semantic-parent=\"5\" data-semantic-role=\"multiplication\" data-semantic-type=\"operator\"></mo><mi data-semantic-=\"\" data-semantic-annotation=\"clearspeak:simple\" data-semantic-font=\"normal\" data-semantic-parent=\"5\" data-semantic-role=\"latinletter\" data-semantic-type=\"identifier\" mathvariant=\"normal\">O</mi></mrow>$ {{\\mathrm{H}}_2}{\\mathrm{O}}$</annotation></semantics></math></mjx-assistive-mml></mjx-container>) flow across a Riga plate, considering influential factors like radiation, exponential heat source, viscous dissipation, magnetic field, and activation energy. The governing equations are modified into ordinary differential equations by employing similarity transformation, The bvp4c solver in MATLAB is used to solve differential equations to obtain the numerical solution. The range of non-dimensional parameters 0.1 < Z < 1, 0 < Kp < 0.5, 1 < R < 5, 0.1 < Ec < 0.4, 0.1 < <span data-altimg=\"/cms/asset/61db4efd-251c-4051-87f8-25f3811f4ccb/adts70009-math-0003.png\"></span><mjx-container ctxtmenu_counter=\"12\" ctxtmenu_oldtabindex=\"1\" jax=\"CHTML\" role=\"application\" sre-explorer- style=\"font-size: 103%; position: relative;\" tabindex=\"0\"><mjx-math aria-hidden=\"true\" location=\"graphic/adts70009-math-0003.png\"><mjx-semantics><mjx-msub data-semantic-children=\"0,1\" data-semantic- data-semantic-role=\"greekletter\" data-semantic-speech=\"phi 1\" data-semantic-type=\"subscript\"><mjx-mi data-semantic-annotation=\"clearspeak:simple\" data-semantic-font=\"italic\" data-semantic- data-semantic-parent=\"2\" data-semantic-role=\"greekletter\" data-semantic-type=\"identifier\"><mjx-c></mjx-c></mjx-mi><mjx-script style=\"vertical-align: -0.15em;\"><mjx-mn data-semantic-annotation=\"clearspeak:simple\" data-semantic-font=\"normal\" data-semantic- data-semantic-parent=\"2\" data-semantic-role=\"integer\" data-semantic-type=\"number\" size=\"s\"><mjx-c></mjx-c></mjx-mn></mjx-script></mjx-msub></mjx-semantics></mjx-math><mjx-assistive-mml display=\"inline\" unselectable=\"on\"><math altimg=\"urn:x-wiley:25130390:media:adts70009:adts70009-math-0003\" display=\"inline\" location=\"graphic/adts70009-math-0003.png\" xmlns=\"http://www.w3.org/1998/Math/MathML\"><semantics><msub data-semantic-=\"\" data-semantic-children=\"0,1\" data-semantic-role=\"greekletter\" data-semantic-speech=\"phi 1\" data-semantic-type=\"subscript\"><mi data-semantic-=\"\" data-semantic-annotation=\"clearspeak:simple\" data-semantic-font=\"italic\" data-semantic-parent=\"2\" data-semantic-role=\"greekletter\" data-semantic-type=\"identifier\">φ</mi><mn data-semantic-=\"\" data-semantic-annotation=\"clearspeak:simple\" data-semantic-font=\"normal\" data-semantic-parent=\"2\" data-semantic-role=\"integer\" data-semantic-type=\"number\">1</mn></msub>${\\varphi _1}$</annotation></semantics></math></mjx-assistive-mml></mjx-container> < 0.4, 0.1 < <span data-altimg=\"/cms/asset/9e82d65f-9fea-47ac-9d4d-753b90f5b150/adts70009-math-0004.png\"></span><mjx-container ctxtmenu_counter=\"13\" ctxtmenu_oldtabindex=\"1\" jax=\"CHTML\" role=\"application\" sre-explorer- style=\"font-size: 103%; position: relative;\" tabindex=\"0\"><mjx-math aria-hidden=\"true\" location=\"graphic/adts70009-math-0004.png\"><mjx-semantics><mjx-msub data-semantic-children=\"0,1\" data-semantic- data-semantic-role=\"greekletter\" data-semantic-speech=\"phi 2\" data-semantic-type=\"subscript\"><mjx-mi data-semantic-annotation=\"clearspeak:simple\" data-semantic-font=\"italic\" data-semantic- data-semantic-parent=\"2\" data-semantic-role=\"greekletter\" data-semantic-type=\"identifier\"><mjx-c></mjx-c></mjx-mi><mjx-script style=\"vertical-align: -0.15em;\"><mjx-mn data-semantic-annotation=\"clearspeak:simple\" data-semantic-font=\"normal\" data-semantic- data-semantic-parent=\"2\" data-semantic-role=\"integer\" data-semantic-type=\"number\" size=\"s\"><mjx-c></mjx-c></mjx-mn></mjx-script></mjx-msub></mjx-semantics></mjx-math><mjx-assistive-mml display=\"inline\" unselectable=\"on\"><math altimg=\"urn:x-wiley:25130390:media:adts70009:adts70009-math-0004\" display=\"inline\" location=\"graphic/adts70009-math-0004.png\" xmlns=\"http://www.w3.org/1998/Math/MathML\"><semantics><msub data-semantic-=\"\" data-semantic-children=\"0,1\" data-semantic-role=\"greekletter\" data-semantic-speech=\"phi 2\" data-semantic-type=\"subscript\"><mi data-semantic-=\"\" data-semantic-annotation=\"clearspeak:simple\" data-semantic-font=\"italic\" data-semantic-parent=\"2\" data-semantic-role=\"greekletter\" data-semantic-type=\"identifier\">φ</mi><mn data-semantic-=\"\" data-semantic-annotation=\"clearspeak:simple\" data-semantic-font=\"normal\" data-semantic-parent=\"2\" data-semantic-role=\"integer\" data-semantic-type=\"number\">2</mn></msub>${\\varphi _2}$</annotation></semantics></math></mjx-assistive-mml></mjx-container> < 0.4, 0.1 < <span data-altimg=\"/cms/asset/680a4b69-6012-4b4b-bb47-f00bf6503fde/adts70009-math-0005.png\"></span><mjx-container ctxtmenu_counter=\"14\" ctxtmenu_oldtabindex=\"1\" jax=\"CHTML\" role=\"application\" sre-explorer- style=\"font-size: 103%; position: relative;\" tabindex=\"0\"><mjx-math aria-hidden=\"true\" location=\"graphic/adts70009-math-0005.png\"><mjx-semantics><mjx-msub data-semantic-children=\"0,1\" data-semantic- data-semantic-role=\"latinletter\" data-semantic-speech=\"upper Q Subscript upper E\" data-semantic-type=\"subscript\"><mjx-mi data-semantic-annotation=\"clearspeak:simple\" data-semantic-font=\"italic\" data-semantic- data-semantic-parent=\"2\" data-semantic-role=\"latinletter\" data-semantic-type=\"identifier\"><mjx-c></mjx-c></mjx-mi><mjx-script style=\"vertical-align: -0.15em;\"><mjx-mi data-semantic-annotation=\"clearspeak:simple\" data-semantic-font=\"italic\" data-semantic- data-semantic-parent=\"2\" data-semantic-role=\"latinletter\" data-semantic-type=\"identifier\" size=\"s\"><mjx-c></mjx-c></mjx-mi></mjx-script></mjx-msub></mjx-semantics></mjx-math><mjx-assistive-mml display=\"inline\" unselectable=\"on\"><math altimg=\"urn:x-wiley:25130390:media:adts70009:adts70009-math-0005\" display=\"inline\" location=\"graphic/adts70009-math-0005.png\" xmlns=\"http://www.w3.org/1998/Math/MathML\"><semantics><msub data-semantic-=\"\" data-semantic-children=\"0,1\" data-semantic-role=\"latinletter\" data-semantic-speech=\"upper Q Subscript upper E\" data-semantic-type=\"subscript\"><mi data-semantic-=\"\" data-semantic-annotation=\"clearspeak:simple\" data-semantic-font=\"italic\" data-semantic-parent=\"2\" data-semantic-role=\"latinletter\" data-semantic-type=\"identifier\">Q</mi><mi data-semantic-=\"\" data-semantic-annotation=\"clearspeak:simple\" data-semantic-font=\"italic\" data-semantic-parent=\"2\" data-semantic-role=\"latinletter\" data-semantic-type=\"identifier\">E</mi></msub>${Q_E}$</annotation></semantics></math></mjx-assistive-mml></mjx-container> < 0.4, 0.1 < Bi < 0.4, 1 < <span data-altimg=\"/cms/asset/8f886440-f812-438f-a39f-a31188dcbf32/adts70009-math-0006.png\"></span><mjx-container ctxtmenu_counter=\"15\" ctxtmenu_oldtabindex=\"1\" jax=\"CHTML\" role=\"application\" sre-explorer- style=\"font-size: 103%; position: relative;\" tabindex=\"0\"><mjx-math aria-hidden=\"true\" location=\"graphic/adts70009-math-0006.png\"><mjx-semantics><mjx-mrow data-semantic-annotation=\"clearspeak:unit\" data-semantic-children=\"0,3\" data-semantic-content=\"4\" data-semantic- data-semantic-role=\"implicit\" data-semantic-speech=\"upper R e Subscript x\" data-semantic-type=\"infixop\"><mjx-mi data-semantic-annotation=\"clearspeak:simple\" data-semantic-font=\"italic\" data-semantic- data-semantic-parent=\"5\" data-semantic-role=\"latinletter\" data-semantic-type=\"identifier\"><mjx-c></mjx-c></mjx-mi><mjx-mo data-semantic-added=\"true\" data-semantic- data-semantic-operator=\"infixop,\" data-semantic-parent=\"5\" data-semantic-role=\"multiplication\" data-semantic-type=\"operator\" style=\"margin-left: 0.056em; margin-right: 0.056em;\"><mjx-c></mjx-c></mjx-mo><mjx-msub data-semantic-children=\"1,2\" data-semantic- data-semantic-parent=\"5\" data-semantic-role=\"latinletter\" data-semantic-type=\"subscript\"><mjx-mi data-semantic-annotation=\"clearspeak:simple\" data-semantic-font=\"italic\" data-semantic- data-semantic-parent=\"3\" data-semantic-role=\"latinletter\" data-semantic-type=\"identifier\"><mjx-c></mjx-c></mjx-mi><mjx-script style=\"vertical-align: -0.15em;\"><mjx-mi data-semantic-annotation=\"clearspeak:simple\" data-semantic-font=\"italic\" data-semantic- data-semantic-parent=\"3\" data-semantic-role=\"latinletter\" data-semantic-type=\"identifier\" size=\"s\"><mjx-c></mjx-c></mjx-mi></mjx-script></mjx-msub></mjx-mrow></mjx-semantics></mjx-math><mjx-assistive-mml display=\"inline\" unselectable=\"on\"><math altimg=\"urn:x-wiley:25130390:media:adts70009:adts70009-math-0006\" display=\"inline\" location=\"graphic/adts70009-math-0006.png\" xmlns=\"http://www.w3.org/1998/Math/MathML\"><semantics><mrow data-semantic-=\"\" data-semantic-annotation=\"clearspeak:unit\" data-semantic-children=\"0,3\" data-semantic-content=\"4\" data-semantic-role=\"implicit\" data-semantic-speech=\"upper R e Subscript x\" data-semantic-type=\"infixop\"><mi data-semantic-=\"\" data-semantic-annotation=\"clearspeak:simple\" data-semantic-font=\"italic\" data-semantic-parent=\"5\" data-semantic-role=\"latinletter\" data-semantic-type=\"identifier\">R</mi><mo data-semantic-=\"\" data-semantic-added=\"true\" data-semantic-operator=\"infixop,\" data-semantic-parent=\"5\" data-semantic-role=\"multiplication\" data-semantic-type=\"operator\"></mo><msub data-semantic-=\"\" data-semantic-children=\"1,2\" data-semantic-parent=\"5\" data-semantic-role=\"latinletter\" data-semantic-type=\"subscript\"><mi data-semantic-=\"\" data-semantic-annotation=\"clearspeak:simple\" data-semantic-font=\"italic\" data-semantic-parent=\"3\" data-semantic-role=\"latinletter\" data-semantic-type=\"identifier\">e</mi><mi data-semantic-=\"\" data-semantic-annotation=\"clearspeak:simple\" data-semantic-font=\"italic\" data-semantic-parent=\"3\" data-semantic-role=\"latinletter\" data-semantic-type=\"identifier\">x</mi></msub></mrow>$R{e_x}$</annotation></semantics></math></mjx-assistive-mml></mjx-container> < 5, and 0.1 < 𝛾 < 0.7. It is detected that temperature distribution enhances with the rise of Hartmann number and radiation, whereas velocity distribution increases with the rise of modified Hartmann number. As activation energy is raised, the concentration profile is also enhanced. Nusselt number increases with a rise of exponential heat source, for numerical values <span data-altimg=\"/cms/asset/36b9bd0e-5ca2-4f74-b4cf-7538af5dc89f/adts70009-math-0007.png\"></span><mjx-container ctxtmenu_counter=\"16\" ctxtmenu_oldtabindex=\"1\" jax=\"CHTML\" role=\"application\" sre-explorer- style=\"font-size: 103%; position: relative;\" tabindex=\"0\"><mjx-math aria-hidden=\"true\" location=\"graphic/adts70009-math-0007.png\"><mjx-semantics><mjx-msub data-semantic-children=\"0,1\" data-semantic- data-semantic-role=\"latinletter\" data-semantic-speech=\"upper Q Subscript normal upper E\" data-semantic-type=\"subscript\"><mjx-mi data-semantic-annotation=\"clearspeak:simple\" data-semantic-font=\"italic\" data-semantic- data-semantic-parent=\"2\" data-semantic-role=\"latinletter\" data-semantic-type=\"identifier\"><mjx-c></mjx-c></mjx-mi><mjx-script style=\"vertical-align: -0.15em;\"><mjx-mi data-semantic-annotation=\"clearspeak:simple\" data-semantic-font=\"normal\" data-semantic- data-semantic-parent=\"2\" data-semantic-role=\"latinletter\" data-semantic-type=\"identifier\" size=\"s\"><mjx-c></mjx-c></mjx-mi></mjx-script></mjx-msub></mjx-semantics></mjx-math><mjx-assistive-mml display=\"inline\" unselectable=\"on\"><math altimg=\"urn:x-wiley:25130390:media:adts70009:adts70009-math-0007\" display=\"inline\" location=\"graphic/adts70009-math-0007.png\" xmlns=\"http://www.w3.org/1998/Math/MathML\"><semantics><msub data-semantic-=\"\" data-semantic-children=\"0,1\" data-semantic-role=\"latinletter\" data-semantic-speech=\"upper Q Subscript normal upper E\" data-semantic-type=\"subscript\"><mi data-semantic-=\"\" data-semantic-annotation=\"clearspeak:simple\" data-semantic-font=\"italic\" data-semantic-parent=\"2\" data-semantic-role=\"latinletter\" data-semantic-type=\"identifier\">Q</mi><mi data-semantic-=\"\" data-semantic-annotation=\"clearspeak:simple\" data-semantic-font=\"normal\" data-semantic-parent=\"2\" data-semantic-role=\"latinletter\" data-semantic-type=\"identifier\" mathvariant=\"normal\">E</mi></msub>${Q_{\\mathrm{E}}}$</annotation></semantics></math></mjx-assistive-mml></mjx-container> = 0.2 and <span data-altimg=\"/cms/asset/f1bbab0c-123d-43ce-8775-a9af6df95694/adts70009-math-0008.png\"></span><mjx-container ctxtmenu_counter=\"17\" ctxtmenu_oldtabindex=\"1\" jax=\"CHTML\" role=\"application\" sre-explorer- style=\"font-size: 103%; position: relative;\" tabindex=\"0\"><mjx-math aria-hidden=\"true\" location=\"graphic/adts70009-math-0008.png\"><mjx-semantics><mjx-msub data-semantic-children=\"0,1\" data-semantic- data-semantic-role=\"latinletter\" data-semantic-speech=\"upper Q Subscript normal upper E\" data-semantic-type=\"subscript\"><mjx-mi data-semantic-annotation=\"clearspeak:simple\" data-semantic-font=\"italic\" data-semantic- data-semantic-parent=\"2\" data-semantic-role=\"latinletter\" data-semantic-type=\"identifier\"><mjx-c></mjx-c></mjx-mi><mjx-script style=\"vertical-align: -0.15em;\"><mjx-mi data-semantic-annotation=\"clearspeak:simple\" data-semantic-font=\"normal\" data-semantic- data-semantic-parent=\"2\" data-semantic-role=\"latinletter\" data-semantic-type=\"identifier\" size=\"s\"><mjx-c></mjx-c></mjx-mi></mjx-script></mjx-msub></mjx-semantics></mjx-math><mjx-assistive-mml display=\"inline\" unselectable=\"on\"><math altimg=\"urn:x-wiley:25130390:media:adts70009:adts70009-math-0008\" display=\"inline\" location=\"graphic/adts70009-math-0008.png\" xmlns=\"http://www.w3.org/1998/Math/MathML\"><semantics><msub data-semantic-=\"\" data-semantic-children=\"0,1\" data-semantic-role=\"latinletter\" data-semantic-speech=\"upper Q Subscript normal upper E\" data-semantic-type=\"subscript\"><mi data-semantic-=\"\" data-semantic-annotation=\"clearspeak:simple\" data-semantic-font=\"italic\" data-semantic-parent=\"2\" data-semantic-role=\"latinletter\" data-semantic-type=\"identifier\">Q</mi><mi data-semantic-=\"\" data-semantic-annotation=\"clearspeak:simple\" data-semantic-font=\"normal\" data-semantic-parent=\"2\" data-semantic-role=\"latinletter\" data-semantic-type=\"identifier\" mathvariant=\"normal\">E</mi></msub>${Q_{\\mathrm{E}}}$</annotation></semantics></math></mjx-assistive-mml></mjx-container> = 0.3. The corresponding Nusselt numbers are 2.8232 <span data-altimg=\"/cms/asset/9c04f7bc-dfd7-4ed9-bbca-c7af5beda223/adts70009-math-0009.png\"></span><mjx-container ctxtmenu_counter=\"18\" ctxtmenu_oldtabindex=\"1\" jax=\"CHTML\" role=\"application\" sre-explorer- style=\"font-size: 103%; position: relative;\" tabindex=\"0\"><mjx-math aria-hidden=\"true\" location=\"graphic/adts70009-math-0009.png\"><mjx-semantics><mjx-mrow data-semantic-children=\"6\" data-semantic-content=\"0\" data-semantic- data-semantic-role=\"unknown\" data-semantic-speech=\"times 10 Superscript negative 0.7\" data-semantic-type=\"prefixop\"><mjx-mo data-semantic- data-semantic-operator=\"prefixop,×\" data-semantic-parent=\"7\" data-semantic-role=\"unknown\" data-semantic-type=\"operator\" rspace=\"4\" space=\"4\"><mjx-c></mjx-c></mjx-mo><mjx-mspace style=\"width: 0.33em;\"></mjx-mspace><mjx-msup data-semantic-children=\"2,5\" data-semantic- data-semantic-parent=\"7\" data-semantic-role=\"integer\" data-semantic-type=\"superscript\"><mjx-mn data-semantic-annotation=\"clearspeak:simple\" data-semantic-font=\"normal\" data-semantic- data-semantic-parent=\"6\" data-semantic-role=\"integer\" data-semantic-type=\"number\"><mjx-c></mjx-c><mjx-c></mjx-c></mjx-mn><mjx-script style=\"vertical-align: 0.393em;\"><mjx-mrow data-semantic-annotation=\"clearspeak:simple\" data-semantic-children=\"4\" data-semantic-content=\"3\" data-semantic- data-semantic-parent=\"6\" data-semantic-role=\"negative\" data-semantic-type=\"prefixop\" size=\"s\"><mjx-mo data-semantic- data-semantic-operator=\"prefixop,−\" data-semantic-parent=\"5\" data-semantic-role=\"subtraction\" data-semantic-type=\"operator\" rspace=\"1\"><mjx-c></mjx-c></mjx-mo><mjx-mn data-semantic-annotation=\"clearspeak:simple\" data-semantic-font=\"normal\" data-semantic- data-semantic-parent=\"5\" data-semantic-role=\"float\" data-semantic-type=\"number\"><mjx-c></mjx-c><mjx-c></mjx-c><mjx-c></mjx-c></mjx-mn></mjx-mrow></mjx-script></mjx-msup></mjx-mrow></mjx-semantics></mjx-math><mjx-assistive-mml display=\"inline\" unselectable=\"on\"><math altimg=\"urn:x-wiley:25130390:media:adts70009:adts70009-math-0009\" display=\"inline\" location=\"graphic/adts70009-math-0009.png\" xmlns=\"http://www.w3.org/1998/Math/MathML\"><semantics><mrow data-semantic-=\"\" data-semantic-children=\"6\" data-semantic-content=\"0\" data-semantic-role=\"unknown\" data-semantic-speech=\"times 10 Superscript negative 0.7\" data-semantic-type=\"prefixop\"><mo data-semantic-=\"\" data-semantic-operator=\"prefixop,×\" data-semantic-parent=\"7\" data-semantic-role=\"unknown\" data-semantic-type=\"operator\">×</mo><mspace width=\"0.33em\"></mspace><msup data-semantic-=\"\" data-semantic-children=\"2,5\" data-semantic-parent=\"7\" data-semantic-role=\"integer\" data-semantic-type=\"superscript\"><mn data-semantic-=\"\" data-semantic-annotation=\"clearspeak:simple\" data-semantic-font=\"normal\" data-semantic-parent=\"6\" data-semantic-role=\"integer\" data-semantic-type=\"number\">10</mn><mrow data-semantic-=\"\" data-semantic-annotation=\"clearspeak:simple\" data-semantic-children=\"4\" data-semantic-content=\"3\" data-semantic-parent=\"6\" data-semantic-role=\"negative\" data-semantic-type=\"prefixop\"><mo data-semantic-=\"\" data-semantic-operator=\"prefixop,−\" data-semantic-parent=\"5\" data-semantic-role=\"subtraction\" data-semantic-type=\"operator\">−</mo><mn data-semantic-=\"\" data-semantic-annotation=\"clearspeak:simple\" data-semantic-font=\"normal\" data-semantic-parent=\"5\" data-semantic-role=\"float\" data-semantic-type=\"number\">0.7</mn></mrow></msup></mrow>$ \\times\\ {10^{ - 0.7}}$</annotation></semantics></math></mjx-assistive-mml></mjx-container> and 5.5421 <span data-altimg=\"/cms/asset/0c3733e9-a252-4030-b6fc-8be41093d005/adts70009-math-0010.png\"></span><mjx-container ctxtmenu_counter=\"19\" ctxtmenu_oldtabindex=\"1\" jax=\"CHTML\" role=\"application\" sre-explorer- style=\"font-size: 103%; position: relative;\" tabindex=\"0\"><mjx-math aria-hidden=\"true\" location=\"graphic/adts70009-math-0010.png\"><mjx-semantics><mjx-mrow data-semantic-children=\"6\" data-semantic-content=\"0\" data-semantic- data-semantic-role=\"unknown\" data-semantic-speech=\"times 10 Superscript negative 0.7\" data-semantic-type=\"prefixop\"><mjx-mo data-semantic- data-semantic-operator=\"prefixop,×\" data-semantic-parent=\"7\" data-semantic-role=\"unknown\" data-semantic-type=\"operator\" rspace=\"4\" space=\"4\"><mjx-c></mjx-c></mjx-mo><mjx-mspace style=\"width: 0.33em;\"></mjx-mspace><mjx-msup data-semantic-children=\"2,5\" data-semantic- data-semantic-parent=\"7\" data-semantic-role=\"integer\" data-semantic-type=\"superscript\"><mjx-mn data-semantic-annotation=\"clearspeak:simple\" data-semantic-font=\"normal\" data-semantic- data-semantic-parent=\"6\" data-semantic-role=\"integer\" data-semantic-type=\"number\"><mjx-c></mjx-c><mjx-c></mjx-c></mjx-mn><mjx-script style=\"vertical-align: 0.393em;\"><mjx-mrow data-semantic-annotation=\"clearspeak:simple\" data-semantic-children=\"4\" data-semantic-content=\"3\" data-semantic- data-semantic-parent=\"6\" data-semantic-role=\"negative\" data-semantic-type=\"prefixop\" size=\"s\"><mjx-mo data-semantic- data-semantic-operator=\"prefixop,−\" data-semantic-parent=\"5\" data-semantic-role=\"subtraction\" data-semantic-type=\"operator\" rspace=\"1\"><mjx-c></mjx-c></mjx-mo><mjx-mn data-semantic-annotation=\"clearspeak:simple\" data-semantic-font=\"normal\" data-semantic- data-semantic-parent=\"5\" data-semantic-role=\"float\" data-semantic-type=\"number\"><mjx-c></mjx-c><mjx-c></mjx-c><mjx-c></mjx-c></mjx-mn></mjx-mrow></mjx-script></mjx-msup></mjx-mrow></mjx-semantics></mjx-math><mjx-assistive-mml display=\"inline\" unselectable=\"on\"><math altimg=\"urn:x-wiley:25130390:media:adts70009:adts70009-math-0010\" display=\"inline\" location=\"graphic/adts70009-math-0010.png\" xmlns=\"http://www.w3.org/1998/Math/MathML\"><semantics><mrow data-semantic-=\"\" data-semantic-children=\"6\" data-semantic-content=\"0\" data-semantic-role=\"unknown\" data-semantic-speech=\"times 10 Superscript negative 0.7\" data-semantic-type=\"prefixop\"><mo data-semantic-=\"\" data-semantic-operator=\"prefixop,×\" data-semantic-parent=\"7\" data-semantic-role=\"unknown\" data-semantic-type=\"operator\">×</mo><mspace width=\"0.33em\"></mspace><msup data-semantic-=\"\" data-semantic-children=\"2,5\" data-semantic-parent=\"7\" data-semantic-role=\"integer\" data-semantic-type=\"superscript\"><mn data-semantic-=\"\" data-semantic-annotation=\"clearspeak:simple\" data-semantic-font=\"normal\" data-semantic-parent=\"6\" data-semantic-role=\"integer\" data-semantic-type=\"number\">10</mn><mrow data-semantic-=\"\" data-semantic-annotation=\"clearspeak:simple\" data-semantic-children=\"4\" data-semantic-content=\"3\" data-semantic-parent=\"6\" data-semantic-role=\"negative\" data-semantic-type=\"prefixop\"><mo data-semantic-=\"\" data-semantic-operator=\"prefixop,−\" data-semantic-parent=\"5\" data-semantic-role=\"subtraction\" data-semantic-type=\"operator\">−</mo><mn data-semantic-=\"\" data-semantic-annotation=\"clearspeak:simple\" data-semantic-font=\"normal\" data-semantic-parent=\"5\" data-semantic-role=\"float\" data-semantic-type=\"number\">0.7</mn></mrow></msup></mrow>$ \\times\\ {10^{ - 0.7}}$</annotation></semantics></math></mjx-assistive-mml></mjx-container>, respectively. The hybrid nanofluid flows over the Riga plate has numerous applications in mechanical engineering, including fuel systems, magnetohydrodynamic (MHD) pumps, energy systems, thermal reactors, etc.","PeriodicalId":7219,"journal":{"name":"Advanced Theory and Simulations","volume":"45 1","pages":""},"PeriodicalIF":2.9000,"publicationDate":"2025-05-20","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"","citationCount":"0","resultStr":"{\"title\":\"Numerical Investigation of Thermal and Mass Diffusion Characteristics in Chemically Reactive and Magnetite Cu–Al2O3 Water-Based Hybrid Nanofluid Flow over Riga Plate\",\"authors\":\"Govind, Pooja Sharma, Ravi Chaudhary, B. K. Sharma, Preeti, Faisal Z. Duraihem\",\"doi\":\"10.1002/adts.202500352\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"The existing work intends to explore the thermal and mass diffusion properties in chemically reactive and magnetite hybrid nanofluids (consisting of <span data-altimg=\\\"/cms/asset/f0a514a9-3c88-4a53-bc8c-1ca644cdaa33/adts70009-math-0001.png\\\"></span><mjx-container ctxtmenu_counter=\\\"10\\\" ctxtmenu_oldtabindex=\\\"1\\\" jax=\\\"CHTML\\\" role=\\\"application\\\" sre-explorer- style=\\\"font-size: 103%; position: relative;\\\" tabindex=\\\"0\\\"><mjx-math aria-hidden=\\\"true\\\" location=\\\"graphic/adts70009-math-0001.png\\\"><mjx-semantics><mjx-mrow><mjx-mrow data-semantic-children=\\\"12,8\\\" data-semantic-content=\\\"7\\\" data-semantic- data-semantic-role=\\\"division\\\" data-semantic-speech=\\\"normal upper A normal l 2 normal upper O 3 divided by upper C u\\\" data-semantic-type=\\\"infixop\\\"><mjx-mrow data-semantic-annotation=\\\"clearspeak:unit\\\" data-semantic-children=\\\"0,3,6\\\" data-semantic-content=\\\"10,11\\\" data-semantic- data-semantic-parent=\\\"13\\\" data-semantic-role=\\\"implicit\\\" data-semantic-type=\\\"infixop\\\"><mjx-mi data-semantic-annotation=\\\"clearspeak:simple\\\" data-semantic-font=\\\"normal\\\" data-semantic- data-semantic-parent=\\\"12\\\" data-semantic-role=\\\"latinletter\\\" data-semantic-type=\\\"identifier\\\"><mjx-c></mjx-c></mjx-mi><mjx-mo data-semantic-added=\\\"true\\\" data-semantic- data-semantic-operator=\\\"infixop,\\\" data-semantic-parent=\\\"12\\\" data-semantic-role=\\\"multiplication\\\" data-semantic-type=\\\"operator\\\" style=\\\"margin-left: 0.056em; margin-right: 0.056em;\\\"><mjx-c></mjx-c></mjx-mo><mjx-msub data-semantic-children=\\\"1,2\\\" data-semantic- data-semantic-parent=\\\"12\\\" data-semantic-role=\\\"latinletter\\\" data-semantic-type=\\\"subscript\\\"><mjx-mi data-semantic-annotation=\\\"clearspeak:simple\\\" data-semantic-font=\\\"normal\\\" data-semantic- data-semantic-parent=\\\"3\\\" data-semantic-role=\\\"latinletter\\\" data-semantic-type=\\\"identifier\\\"><mjx-c></mjx-c></mjx-mi><mjx-script style=\\\"vertical-align: -0.15em;\\\"><mjx-mn data-semantic-annotation=\\\"clearspeak:simple\\\" data-semantic-font=\\\"normal\\\" data-semantic- data-semantic-parent=\\\"3\\\" data-semantic-role=\\\"integer\\\" data-semantic-type=\\\"number\\\" size=\\\"s\\\"><mjx-c></mjx-c></mjx-mn></mjx-script></mjx-msub><mjx-mo data-semantic-added=\\\"true\\\" data-semantic- data-semantic-operator=\\\"infixop,\\\" data-semantic-parent=\\\"12\\\" data-semantic-role=\\\"multiplication\\\" data-semantic-type=\\\"operator\\\" style=\\\"margin-left: 0.056em; margin-right: 0.056em;\\\"><mjx-c></mjx-c></mjx-mo><mjx-msub data-semantic-children=\\\"4,5\\\" data-semantic- data-semantic-parent=\\\"12\\\" data-semantic-role=\\\"latinletter\\\" data-semantic-type=\\\"subscript\\\"><mjx-mi data-semantic-annotation=\\\"clearspeak:simple\\\" data-semantic-font=\\\"normal\\\" data-semantic- data-semantic-parent=\\\"6\\\" data-semantic-role=\\\"latinletter\\\" data-semantic-type=\\\"identifier\\\"><mjx-c></mjx-c></mjx-mi><mjx-script style=\\\"vertical-align: -0.15em;\\\"><mjx-mn data-semantic-annotation=\\\"clearspeak:simple\\\" data-semantic-font=\\\"normal\\\" data-semantic- data-semantic-parent=\\\"6\\\" data-semantic-role=\\\"integer\\\" data-semantic-type=\\\"number\\\" size=\\\"s\\\"><mjx-c></mjx-c></mjx-mn></mjx-script></mjx-msub></mjx-mrow><mjx-mo data-semantic- data-semantic-operator=\\\"infixop,/\\\" data-semantic-parent=\\\"13\\\" data-semantic-role=\\\"division\\\" data-semantic-type=\\\"operator\\\" rspace=\\\"1\\\" space=\\\"1\\\"><mjx-c></mjx-c></mjx-mo><mjx-mi data-semantic-font=\\\"normal\\\" data-semantic- data-semantic-parent=\\\"13\\\" data-semantic-role=\\\"unknown\\\" data-semantic-type=\\\"identifier\\\"><mjx-c></mjx-c><mjx-c></mjx-c></mjx-mi></mjx-mrow><mjx-mspace style=\\\"width: 0.28em;\\\"></mjx-mspace></mjx-mrow></mjx-semantics></mjx-math><mjx-assistive-mml display=\\\"inline\\\" unselectable=\\\"on\\\"><math altimg=\\\"urn:x-wiley:25130390:media:adts70009:adts70009-math-0001\\\" display=\\\"inline\\\" location=\\\"graphic/adts70009-math-0001.png\\\" xmlns=\\\"http://www.w3.org/1998/Math/MathML\\\"><semantics><mrow><mrow data-semantic-=\\\"\\\" data-semantic-children=\\\"12,8\\\" data-semantic-content=\\\"7\\\" data-semantic-role=\\\"division\\\" data-semantic-speech=\\\"normal upper A normal l 2 normal upper O 3 divided by upper C u\\\" data-semantic-type=\\\"infixop\\\"><mrow data-semantic-=\\\"\\\" data-semantic-annotation=\\\"clearspeak:unit\\\" data-semantic-children=\\\"0,3,6\\\" data-semantic-content=\\\"10,11\\\" data-semantic-parent=\\\"13\\\" data-semantic-role=\\\"implicit\\\" data-semantic-type=\\\"infixop\\\"><mi data-semantic-=\\\"\\\" data-semantic-annotation=\\\"clearspeak:simple\\\" data-semantic-font=\\\"normal\\\" data-semantic-parent=\\\"12\\\" data-semantic-role=\\\"latinletter\\\" data-semantic-type=\\\"identifier\\\" mathvariant=\\\"normal\\\">A</mi><mo data-semantic-=\\\"\\\" data-semantic-added=\\\"true\\\" data-semantic-operator=\\\"infixop,\\\" data-semantic-parent=\\\"12\\\" data-semantic-role=\\\"multiplication\\\" data-semantic-type=\\\"operator\\\"></mo><msub data-semantic-=\\\"\\\" data-semantic-children=\\\"1,2\\\" data-semantic-parent=\\\"12\\\" data-semantic-role=\\\"latinletter\\\" data-semantic-type=\\\"subscript\\\"><mi data-semantic-=\\\"\\\" data-semantic-annotation=\\\"clearspeak:simple\\\" data-semantic-font=\\\"normal\\\" data-semantic-parent=\\\"3\\\" data-semantic-role=\\\"latinletter\\\" data-semantic-type=\\\"identifier\\\" mathvariant=\\\"normal\\\">l</mi><mn data-semantic-=\\\"\\\" data-semantic-annotation=\\\"clearspeak:simple\\\" data-semantic-font=\\\"normal\\\" data-semantic-parent=\\\"3\\\" data-semantic-role=\\\"integer\\\" data-semantic-type=\\\"number\\\">2</mn></msub><mo data-semantic-=\\\"\\\" data-semantic-added=\\\"true\\\" data-semantic-operator=\\\"infixop,\\\" data-semantic-parent=\\\"12\\\" data-semantic-role=\\\"multiplication\\\" data-semantic-type=\\\"operator\\\"></mo><msub data-semantic-=\\\"\\\" data-semantic-children=\\\"4,5\\\" data-semantic-parent=\\\"12\\\" data-semantic-role=\\\"latinletter\\\" data-semantic-type=\\\"subscript\\\"><mi data-semantic-=\\\"\\\" data-semantic-annotation=\\\"clearspeak:simple\\\" data-semantic-font=\\\"normal\\\" data-semantic-parent=\\\"6\\\" data-semantic-role=\\\"latinletter\\\" data-semantic-type=\\\"identifier\\\" mathvariant=\\\"normal\\\">O</mi><mn data-semantic-=\\\"\\\" data-semantic-annotation=\\\"clearspeak:simple\\\" data-semantic-font=\\\"normal\\\" data-semantic-parent=\\\"6\\\" data-semantic-role=\\\"integer\\\" data-semantic-type=\\\"number\\\">3</mn></msub></mrow><mo data-semantic-=\\\"\\\" data-semantic-operator=\\\"infixop,/\\\" data-semantic-parent=\\\"13\\\" data-semantic-role=\\\"division\\\" data-semantic-type=\\\"operator\\\">/</mo><mi data-semantic-=\\\"\\\" data-semantic-font=\\\"normal\\\" data-semantic-parent=\\\"13\\\" data-semantic-role=\\\"unknown\\\" data-semantic-type=\\\"identifier\\\">Cu</mi></mrow><mspace width=\\\"0.28em\\\"></mspace></mrow>${\\\\mathrm{A}}{{\\\\mathrm{l}}_{2 }}{{\\\\mathrm{O}}_3}/{\\\\mathrm{Cu}}\\\\;$</annotation></semantics></math></mjx-assistive-mml></mjx-container> nanoparticles dispersed in <span data-altimg=\\\"/cms/asset/437e1cb3-62db-4991-a939-035e4b38558d/adts70009-math-0002.png\\\"></span><mjx-container ctxtmenu_counter=\\\"11\\\" ctxtmenu_oldtabindex=\\\"1\\\" jax=\\\"CHTML\\\" role=\\\"application\\\" sre-explorer- style=\\\"font-size: 103%; position: relative;\\\" tabindex=\\\"0\\\"><mjx-math aria-hidden=\\\"true\\\" location=\\\"graphic/adts70009-math-0002.png\\\"><mjx-semantics><mjx-mrow data-semantic-annotation=\\\"clearspeak:unit\\\" data-semantic-children=\\\"2,3\\\" data-semantic-content=\\\"4\\\" data-semantic- data-semantic-role=\\\"implicit\\\" data-semantic-speech=\\\"normal upper H 2 normal upper O\\\" data-semantic-type=\\\"infixop\\\"><mjx-msub data-semantic-children=\\\"0,1\\\" data-semantic- data-semantic-parent=\\\"5\\\" data-semantic-role=\\\"latinletter\\\" data-semantic-type=\\\"subscript\\\"><mjx-mi data-semantic-annotation=\\\"clearspeak:simple\\\" data-semantic-font=\\\"normal\\\" data-semantic- data-semantic-parent=\\\"2\\\" data-semantic-role=\\\"latinletter\\\" data-semantic-type=\\\"identifier\\\"><mjx-c></mjx-c></mjx-mi><mjx-script style=\\\"vertical-align: -0.15em;\\\"><mjx-mn data-semantic-annotation=\\\"clearspeak:simple\\\" data-semantic-font=\\\"normal\\\" data-semantic- data-semantic-parent=\\\"2\\\" data-semantic-role=\\\"integer\\\" data-semantic-type=\\\"number\\\" size=\\\"s\\\"><mjx-c></mjx-c></mjx-mn></mjx-script></mjx-msub><mjx-mo data-semantic-added=\\\"true\\\" data-semantic- data-semantic-operator=\\\"infixop,\\\" data-semantic-parent=\\\"5\\\" data-semantic-role=\\\"multiplication\\\" data-semantic-type=\\\"operator\\\" style=\\\"margin-left: 0.056em; margin-right: 0.056em;\\\"><mjx-c></mjx-c></mjx-mo><mjx-mi data-semantic-annotation=\\\"clearspeak:simple\\\" data-semantic-font=\\\"normal\\\" data-semantic- data-semantic-parent=\\\"5\\\" data-semantic-role=\\\"latinletter\\\" data-semantic-type=\\\"identifier\\\"><mjx-c></mjx-c></mjx-mi></mjx-mrow></mjx-semantics></mjx-math><mjx-assistive-mml display=\\\"inline\\\" unselectable=\\\"on\\\"><math altimg=\\\"urn:x-wiley:25130390:media:adts70009:adts70009-math-0002\\\" display=\\\"inline\\\" location=\\\"graphic/adts70009-math-0002.png\\\" xmlns=\\\"http://www.w3.org/1998/Math/MathML\\\"><semantics><mrow data-semantic-=\\\"\\\" data-semantic-annotation=\\\"clearspeak:unit\\\" data-semantic-children=\\\"2,3\\\" data-semantic-content=\\\"4\\\" data-semantic-role=\\\"implicit\\\" data-semantic-speech=\\\"normal upper H 2 normal upper O\\\" data-semantic-type=\\\"infixop\\\"><msub data-semantic-=\\\"\\\" data-semantic-children=\\\"0,1\\\" data-semantic-parent=\\\"5\\\" data-semantic-role=\\\"latinletter\\\" data-semantic-type=\\\"subscript\\\"><mi data-semantic-=\\\"\\\" data-semantic-annotation=\\\"clearspeak:simple\\\" data-semantic-font=\\\"normal\\\" data-semantic-parent=\\\"2\\\" data-semantic-role=\\\"latinletter\\\" data-semantic-type=\\\"identifier\\\" mathvariant=\\\"normal\\\">H</mi><mn data-semantic-=\\\"\\\" data-semantic-annotation=\\\"clearspeak:simple\\\" data-semantic-font=\\\"normal\\\" data-semantic-parent=\\\"2\\\" data-semantic-role=\\\"integer\\\" data-semantic-type=\\\"number\\\">2</mn></msub><mo data-semantic-=\\\"\\\" data-semantic-added=\\\"true\\\" data-semantic-operator=\\\"infixop,\\\" data-semantic-parent=\\\"5\\\" data-semantic-role=\\\"multiplication\\\" data-semantic-type=\\\"operator\\\"></mo><mi data-semantic-=\\\"\\\" data-semantic-annotation=\\\"clearspeak:simple\\\" data-semantic-font=\\\"normal\\\" data-semantic-parent=\\\"5\\\" data-semantic-role=\\\"latinletter\\\" data-semantic-type=\\\"identifier\\\" mathvariant=\\\"normal\\\">O</mi></mrow>$ {{\\\\mathrm{H}}_2}{\\\\mathrm{O}}$</annotation></semantics></math></mjx-assistive-mml></mjx-container>) flow across a Riga plate, considering influential factors like radiation, exponential heat source, viscous dissipation, magnetic field, and activation energy. The governing equations are modified into ordinary differential equations by employing similarity transformation, The bvp4c solver in MATLAB is used to solve differential equations to obtain the numerical solution. The range of non-dimensional parameters 0.1 < Z < 1, 0 < Kp < 0.5, 1 < R < 5, 0.1 < Ec < 0.4, 0.1 < <span data-altimg=\\\"/cms/asset/61db4efd-251c-4051-87f8-25f3811f4ccb/adts70009-math-0003.png\\\"></span><mjx-container ctxtmenu_counter=\\\"12\\\" ctxtmenu_oldtabindex=\\\"1\\\" jax=\\\"CHTML\\\" role=\\\"application\\\" sre-explorer- style=\\\"font-size: 103%; position: relative;\\\" tabindex=\\\"0\\\"><mjx-math aria-hidden=\\\"true\\\" location=\\\"graphic/adts70009-math-0003.png\\\"><mjx-semantics><mjx-msub data-semantic-children=\\\"0,1\\\" data-semantic- data-semantic-role=\\\"greekletter\\\" data-semantic-speech=\\\"phi 1\\\" data-semantic-type=\\\"subscript\\\"><mjx-mi data-semantic-annotation=\\\"clearspeak:simple\\\" data-semantic-font=\\\"italic\\\" data-semantic- data-semantic-parent=\\\"2\\\" data-semantic-role=\\\"greekletter\\\" data-semantic-type=\\\"identifier\\\"><mjx-c></mjx-c></mjx-mi><mjx-script style=\\\"vertical-align: -0.15em;\\\"><mjx-mn data-semantic-annotation=\\\"clearspeak:simple\\\" data-semantic-font=\\\"normal\\\" data-semantic- data-semantic-parent=\\\"2\\\" data-semantic-role=\\\"integer\\\" data-semantic-type=\\\"number\\\" size=\\\"s\\\"><mjx-c></mjx-c></mjx-mn></mjx-script></mjx-msub></mjx-semantics></mjx-math><mjx-assistive-mml display=\\\"inline\\\" unselectable=\\\"on\\\"><math altimg=\\\"urn:x-wiley:25130390:media:adts70009:adts70009-math-0003\\\" display=\\\"inline\\\" location=\\\"graphic/adts70009-math-0003.png\\\" xmlns=\\\"http://www.w3.org/1998/Math/MathML\\\"><semantics><msub data-semantic-=\\\"\\\" data-semantic-children=\\\"0,1\\\" data-semantic-role=\\\"greekletter\\\" data-semantic-speech=\\\"phi 1\\\" data-semantic-type=\\\"subscript\\\"><mi data-semantic-=\\\"\\\" data-semantic-annotation=\\\"clearspeak:simple\\\" data-semantic-font=\\\"italic\\\" data-semantic-parent=\\\"2\\\" data-semantic-role=\\\"greekletter\\\" data-semantic-type=\\\"identifier\\\">φ</mi><mn data-semantic-=\\\"\\\" data-semantic-annotation=\\\"clearspeak:simple\\\" data-semantic-font=\\\"normal\\\" data-semantic-parent=\\\"2\\\" data-semantic-role=\\\"integer\\\" data-semantic-type=\\\"number\\\">1</mn></msub>${\\\\varphi _1}$</annotation></semantics></math></mjx-assistive-mml></mjx-container> < 0.4, 0.1 < <span data-altimg=\\\"/cms/asset/9e82d65f-9fea-47ac-9d4d-753b90f5b150/adts70009-math-0004.png\\\"></span><mjx-container ctxtmenu_counter=\\\"13\\\" ctxtmenu_oldtabindex=\\\"1\\\" jax=\\\"CHTML\\\" role=\\\"application\\\" sre-explorer- style=\\\"font-size: 103%; position: relative;\\\" tabindex=\\\"0\\\"><mjx-math aria-hidden=\\\"true\\\" location=\\\"graphic/adts70009-math-0004.png\\\"><mjx-semantics><mjx-msub data-semantic-children=\\\"0,1\\\" data-semantic- data-semantic-role=\\\"greekletter\\\" data-semantic-speech=\\\"phi 2\\\" data-semantic-type=\\\"subscript\\\"><mjx-mi data-semantic-annotation=\\\"clearspeak:simple\\\" data-semantic-font=\\\"italic\\\" data-semantic- data-semantic-parent=\\\"2\\\" data-semantic-role=\\\"greekletter\\\" data-semantic-type=\\\"identifier\\\"><mjx-c></mjx-c></mjx-mi><mjx-script style=\\\"vertical-align: -0.15em;\\\"><mjx-mn data-semantic-annotation=\\\"clearspeak:simple\\\" data-semantic-font=\\\"normal\\\" data-semantic- data-semantic-parent=\\\"2\\\" data-semantic-role=\\\"integer\\\" data-semantic-type=\\\"number\\\" size=\\\"s\\\"><mjx-c></mjx-c></mjx-mn></mjx-script></mjx-msub></mjx-semantics></mjx-math><mjx-assistive-mml display=\\\"inline\\\" unselectable=\\\"on\\\"><math altimg=\\\"urn:x-wiley:25130390:media:adts70009:adts70009-math-0004\\\" display=\\\"inline\\\" location=\\\"graphic/adts70009-math-0004.png\\\" xmlns=\\\"http://www.w3.org/1998/Math/MathML\\\"><semantics><msub data-semantic-=\\\"\\\" data-semantic-children=\\\"0,1\\\" data-semantic-role=\\\"greekletter\\\" data-semantic-speech=\\\"phi 2\\\" data-semantic-type=\\\"subscript\\\"><mi data-semantic-=\\\"\\\" data-semantic-annotation=\\\"clearspeak:simple\\\" data-semantic-font=\\\"italic\\\" data-semantic-parent=\\\"2\\\" data-semantic-role=\\\"greekletter\\\" data-semantic-type=\\\"identifier\\\">φ</mi><mn data-semantic-=\\\"\\\" data-semantic-annotation=\\\"clearspeak:simple\\\" data-semantic-font=\\\"normal\\\" data-semantic-parent=\\\"2\\\" data-semantic-role=\\\"integer\\\" data-semantic-type=\\\"number\\\">2</mn></msub>${\\\\varphi _2}$</annotation></semantics></math></mjx-assistive-mml></mjx-container> < 0.4, 0.1 < <span data-altimg=\\\"/cms/asset/680a4b69-6012-4b4b-bb47-f00bf6503fde/adts70009-math-0005.png\\\"></span><mjx-container ctxtmenu_counter=\\\"14\\\" ctxtmenu_oldtabindex=\\\"1\\\" jax=\\\"CHTML\\\" role=\\\"application\\\" sre-explorer- style=\\\"font-size: 103%; position: relative;\\\" tabindex=\\\"0\\\"><mjx-math aria-hidden=\\\"true\\\" location=\\\"graphic/adts70009-math-0005.png\\\"><mjx-semantics><mjx-msub data-semantic-children=\\\"0,1\\\" data-semantic- data-semantic-role=\\\"latinletter\\\" data-semantic-speech=\\\"upper Q Subscript upper E\\\" data-semantic-type=\\\"subscript\\\"><mjx-mi data-semantic-annotation=\\\"clearspeak:simple\\\" data-semantic-font=\\\"italic\\\" data-semantic- data-semantic-parent=\\\"2\\\" data-semantic-role=\\\"latinletter\\\" data-semantic-type=\\\"identifier\\\"><mjx-c></mjx-c></mjx-mi><mjx-script style=\\\"vertical-align: -0.15em;\\\"><mjx-mi data-semantic-annotation=\\\"clearspeak:simple\\\" data-semantic-font=\\\"italic\\\" data-semantic- data-semantic-parent=\\\"2\\\" data-semantic-role=\\\"latinletter\\\" data-semantic-type=\\\"identifier\\\" size=\\\"s\\\"><mjx-c></mjx-c></mjx-mi></mjx-script></mjx-msub></mjx-semantics></mjx-math><mjx-assistive-mml display=\\\"inline\\\" unselectable=\\\"on\\\"><math altimg=\\\"urn:x-wiley:25130390:media:adts70009:adts70009-math-0005\\\" display=\\\"inline\\\" location=\\\"graphic/adts70009-math-0005.png\\\" xmlns=\\\"http://www.w3.org/1998/Math/MathML\\\"><semantics><msub data-semantic-=\\\"\\\" data-semantic-children=\\\"0,1\\\" data-semantic-role=\\\"latinletter\\\" data-semantic-speech=\\\"upper Q Subscript upper E\\\" data-semantic-type=\\\"subscript\\\"><mi data-semantic-=\\\"\\\" data-semantic-annotation=\\\"clearspeak:simple\\\" data-semantic-font=\\\"italic\\\" data-semantic-parent=\\\"2\\\" data-semantic-role=\\\"latinletter\\\" data-semantic-type=\\\"identifier\\\">Q</mi><mi data-semantic-=\\\"\\\" data-semantic-annotation=\\\"clearspeak:simple\\\" data-semantic-font=\\\"italic\\\" data-semantic-parent=\\\"2\\\" data-semantic-role=\\\"latinletter\\\" data-semantic-type=\\\"identifier\\\">E</mi></msub>${Q_E}$</annotation></semantics></math></mjx-assistive-mml></mjx-container> < 0.4, 0.1 < Bi < 0.4, 1 < <span data-altimg=\\\"/cms/asset/8f886440-f812-438f-a39f-a31188dcbf32/adts70009-math-0006.png\\\"></span><mjx-container ctxtmenu_counter=\\\"15\\\" ctxtmenu_oldtabindex=\\\"1\\\" jax=\\\"CHTML\\\" role=\\\"application\\\" sre-explorer- style=\\\"font-size: 103%; position: relative;\\\" tabindex=\\\"0\\\"><mjx-math aria-hidden=\\\"true\\\" location=\\\"graphic/adts70009-math-0006.png\\\"><mjx-semantics><mjx-mrow data-semantic-annotation=\\\"clearspeak:unit\\\" data-semantic-children=\\\"0,3\\\" data-semantic-content=\\\"4\\\" data-semantic- data-semantic-role=\\\"implicit\\\" data-semantic-speech=\\\"upper R e Subscript x\\\" data-semantic-type=\\\"infixop\\\"><mjx-mi data-semantic-annotation=\\\"clearspeak:simple\\\" data-semantic-font=\\\"italic\\\" data-semantic- data-semantic-parent=\\\"5\\\" data-semantic-role=\\\"latinletter\\\" data-semantic-type=\\\"identifier\\\"><mjx-c></mjx-c></mjx-mi><mjx-mo data-semantic-added=\\\"true\\\" data-semantic- data-semantic-operator=\\\"infixop,\\\" data-semantic-parent=\\\"5\\\" data-semantic-role=\\\"multiplication\\\" data-semantic-type=\\\"operator\\\" style=\\\"margin-left: 0.056em; margin-right: 0.056em;\\\"><mjx-c></mjx-c></mjx-mo><mjx-msub data-semantic-children=\\\"1,2\\\" data-semantic- data-semantic-parent=\\\"5\\\" data-semantic-role=\\\"latinletter\\\" data-semantic-type=\\\"subscript\\\"><mjx-mi data-semantic-annotation=\\\"clearspeak:simple\\\" data-semantic-font=\\\"italic\\\" data-semantic- data-semantic-parent=\\\"3\\\" data-semantic-role=\\\"latinletter\\\" data-semantic-type=\\\"identifier\\\"><mjx-c></mjx-c></mjx-mi><mjx-script style=\\\"vertical-align: -0.15em;\\\"><mjx-mi data-semantic-annotation=\\\"clearspeak:simple\\\" data-semantic-font=\\\"italic\\\" data-semantic- data-semantic-parent=\\\"3\\\" data-semantic-role=\\\"latinletter\\\" data-semantic-type=\\\"identifier\\\" size=\\\"s\\\"><mjx-c></mjx-c></mjx-mi></mjx-script></mjx-msub></mjx-mrow></mjx-semantics></mjx-math><mjx-assistive-mml display=\\\"inline\\\" unselectable=\\\"on\\\"><math altimg=\\\"urn:x-wiley:25130390:media:adts70009:adts70009-math-0006\\\" display=\\\"inline\\\" location=\\\"graphic/adts70009-math-0006.png\\\" xmlns=\\\"http://www.w3.org/1998/Math/MathML\\\"><semantics><mrow data-semantic-=\\\"\\\" data-semantic-annotation=\\\"clearspeak:unit\\\" data-semantic-children=\\\"0,3\\\" data-semantic-content=\\\"4\\\" data-semantic-role=\\\"implicit\\\" data-semantic-speech=\\\"upper R e Subscript x\\\" data-semantic-type=\\\"infixop\\\"><mi data-semantic-=\\\"\\\" data-semantic-annotation=\\\"clearspeak:simple\\\" data-semantic-font=\\\"italic\\\" data-semantic-parent=\\\"5\\\" data-semantic-role=\\\"latinletter\\\" data-semantic-type=\\\"identifier\\\">R</mi><mo data-semantic-=\\\"\\\" data-semantic-added=\\\"true\\\" data-semantic-operator=\\\"infixop,\\\" data-semantic-parent=\\\"5\\\" data-semantic-role=\\\"multiplication\\\" data-semantic-type=\\\"operator\\\"></mo><msub data-semantic-=\\\"\\\" data-semantic-children=\\\"1,2\\\" data-semantic-parent=\\\"5\\\" data-semantic-role=\\\"latinletter\\\" data-semantic-type=\\\"subscript\\\"><mi data-semantic-=\\\"\\\" data-semantic-annotation=\\\"clearspeak:simple\\\" data-semantic-font=\\\"italic\\\" data-semantic-parent=\\\"3\\\" data-semantic-role=\\\"latinletter\\\" data-semantic-type=\\\"identifier\\\">e</mi><mi data-semantic-=\\\"\\\" data-semantic-annotation=\\\"clearspeak:simple\\\" data-semantic-font=\\\"italic\\\" data-semantic-parent=\\\"3\\\" data-semantic-role=\\\"latinletter\\\" data-semantic-type=\\\"identifier\\\">x</mi></msub></mrow>$R{e_x}$</annotation></semantics></math></mjx-assistive-mml></mjx-container> < 5, and 0.1 < 𝛾 < 0.7. It is detected that temperature distribution enhances with the rise of Hartmann number and radiation, whereas velocity distribution increases with the rise of modified Hartmann number. As activation energy is raised, the concentration profile is also enhanced. Nusselt number increases with a rise of exponential heat source, for numerical values <span data-altimg=\\\"/cms/asset/36b9bd0e-5ca2-4f74-b4cf-7538af5dc89f/adts70009-math-0007.png\\\"></span><mjx-container ctxtmenu_counter=\\\"16\\\" ctxtmenu_oldtabindex=\\\"1\\\" jax=\\\"CHTML\\\" role=\\\"application\\\" sre-explorer- style=\\\"font-size: 103%; position: relative;\\\" tabindex=\\\"0\\\"><mjx-math aria-hidden=\\\"true\\\" location=\\\"graphic/adts70009-math-0007.png\\\"><mjx-semantics><mjx-msub data-semantic-children=\\\"0,1\\\" data-semantic- data-semantic-role=\\\"latinletter\\\" data-semantic-speech=\\\"upper Q Subscript normal upper E\\\" data-semantic-type=\\\"subscript\\\"><mjx-mi data-semantic-annotation=\\\"clearspeak:simple\\\" data-semantic-font=\\\"italic\\\" data-semantic- data-semantic-parent=\\\"2\\\" data-semantic-role=\\\"latinletter\\\" data-semantic-type=\\\"identifier\\\"><mjx-c></mjx-c></mjx-mi><mjx-script style=\\\"vertical-align: -0.15em;\\\"><mjx-mi data-semantic-annotation=\\\"clearspeak:simple\\\" data-semantic-font=\\\"normal\\\" data-semantic- data-semantic-parent=\\\"2\\\" data-semantic-role=\\\"latinletter\\\" data-semantic-type=\\\"identifier\\\" size=\\\"s\\\"><mjx-c></mjx-c></mjx-mi></mjx-script></mjx-msub></mjx-semantics></mjx-math><mjx-assistive-mml display=\\\"inline\\\" unselectable=\\\"on\\\"><math altimg=\\\"urn:x-wiley:25130390:media:adts70009:adts70009-math-0007\\\" display=\\\"inline\\\" location=\\\"graphic/adts70009-math-0007.png\\\" xmlns=\\\"http://www.w3.org/1998/Math/MathML\\\"><semantics><msub data-semantic-=\\\"\\\" data-semantic-children=\\\"0,1\\\" data-semantic-role=\\\"latinletter\\\" data-semantic-speech=\\\"upper Q Subscript normal upper E\\\" data-semantic-type=\\\"subscript\\\"><mi data-semantic-=\\\"\\\" data-semantic-annotation=\\\"clearspeak:simple\\\" data-semantic-font=\\\"italic\\\" data-semantic-parent=\\\"2\\\" data-semantic-role=\\\"latinletter\\\" data-semantic-type=\\\"identifier\\\">Q</mi><mi data-semantic-=\\\"\\\" data-semantic-annotation=\\\"clearspeak:simple\\\" data-semantic-font=\\\"normal\\\" data-semantic-parent=\\\"2\\\" data-semantic-role=\\\"latinletter\\\" data-semantic-type=\\\"identifier\\\" mathvariant=\\\"normal\\\">E</mi></msub>${Q_{\\\\mathrm{E}}}$</annotation></semantics></math></mjx-assistive-mml></mjx-container> = 0.2 and <span data-altimg=\\\"/cms/asset/f1bbab0c-123d-43ce-8775-a9af6df95694/adts70009-math-0008.png\\\"></span><mjx-container ctxtmenu_counter=\\\"17\\\" ctxtmenu_oldtabindex=\\\"1\\\" jax=\\\"CHTML\\\" role=\\\"application\\\" sre-explorer- style=\\\"font-size: 103%; position: relative;\\\" tabindex=\\\"0\\\"><mjx-math aria-hidden=\\\"true\\\" location=\\\"graphic/adts70009-math-0008.png\\\"><mjx-semantics><mjx-msub data-semantic-children=\\\"0,1\\\" data-semantic- data-semantic-role=\\\"latinletter\\\" data-semantic-speech=\\\"upper Q Subscript normal upper E\\\" data-semantic-type=\\\"subscript\\\"><mjx-mi data-semantic-annotation=\\\"clearspeak:simple\\\" data-semantic-font=\\\"italic\\\" data-semantic- data-semantic-parent=\\\"2\\\" data-semantic-role=\\\"latinletter\\\" data-semantic-type=\\\"identifier\\\"><mjx-c></mjx-c></mjx-mi><mjx-script style=\\\"vertical-align: -0.15em;\\\"><mjx-mi data-semantic-annotation=\\\"clearspeak:simple\\\" data-semantic-font=\\\"normal\\\" data-semantic- data-semantic-parent=\\\"2\\\" data-semantic-role=\\\"latinletter\\\" data-semantic-type=\\\"identifier\\\" size=\\\"s\\\"><mjx-c></mjx-c></mjx-mi></mjx-script></mjx-msub></mjx-semantics></mjx-math><mjx-assistive-mml display=\\\"inline\\\" unselectable=\\\"on\\\"><math altimg=\\\"urn:x-wiley:25130390:media:adts70009:adts70009-math-0008\\\" display=\\\"inline\\\" location=\\\"graphic/adts70009-math-0008.png\\\" xmlns=\\\"http://www.w3.org/1998/Math/MathML\\\"><semantics><msub data-semantic-=\\\"\\\" data-semantic-children=\\\"0,1\\\" data-semantic-role=\\\"latinletter\\\" data-semantic-speech=\\\"upper Q Subscript normal upper E\\\" data-semantic-type=\\\"subscript\\\"><mi data-semantic-=\\\"\\\" data-semantic-annotation=\\\"clearspeak:simple\\\" data-semantic-font=\\\"italic\\\" data-semantic-parent=\\\"2\\\" data-semantic-role=\\\"latinletter\\\" data-semantic-type=\\\"identifier\\\">Q</mi><mi data-semantic-=\\\"\\\" data-semantic-annotation=\\\"clearspeak:simple\\\" data-semantic-font=\\\"normal\\\" data-semantic-parent=\\\"2\\\" data-semantic-role=\\\"latinletter\\\" data-semantic-type=\\\"identifier\\\" mathvariant=\\\"normal\\\">E</mi></msub>${Q_{\\\\mathrm{E}}}$</annotation></semantics></math></mjx-assistive-mml></mjx-container> = 0.3. The corresponding Nusselt numbers are 2.8232 <span data-altimg=\\\"/cms/asset/9c04f7bc-dfd7-4ed9-bbca-c7af5beda223/adts70009-math-0009.png\\\"></span><mjx-container ctxtmenu_counter=\\\"18\\\" ctxtmenu_oldtabindex=\\\"1\\\" jax=\\\"CHTML\\\" role=\\\"application\\\" sre-explorer- style=\\\"font-size: 103%; position: relative;\\\" tabindex=\\\"0\\\"><mjx-math aria-hidden=\\\"true\\\" location=\\\"graphic/adts70009-math-0009.png\\\"><mjx-semantics><mjx-mrow data-semantic-children=\\\"6\\\" data-semantic-content=\\\"0\\\" data-semantic- data-semantic-role=\\\"unknown\\\" data-semantic-speech=\\\"times 10 Superscript negative 0.7\\\" data-semantic-type=\\\"prefixop\\\"><mjx-mo data-semantic- data-semantic-operator=\\\"prefixop,×\\\" data-semantic-parent=\\\"7\\\" data-semantic-role=\\\"unknown\\\" data-semantic-type=\\\"operator\\\" rspace=\\\"4\\\" space=\\\"4\\\"><mjx-c></mjx-c></mjx-mo><mjx-mspace style=\\\"width: 0.33em;\\\"></mjx-mspace><mjx-msup data-semantic-children=\\\"2,5\\\" data-semantic- data-semantic-parent=\\\"7\\\" data-semantic-role=\\\"integer\\\" data-semantic-type=\\\"superscript\\\"><mjx-mn data-semantic-annotation=\\\"clearspeak:simple\\\" data-semantic-font=\\\"normal\\\" data-semantic- data-semantic-parent=\\\"6\\\" data-semantic-role=\\\"integer\\\" data-semantic-type=\\\"number\\\"><mjx-c></mjx-c><mjx-c></mjx-c></mjx-mn><mjx-script style=\\\"vertical-align: 0.393em;\\\"><mjx-mrow data-semantic-annotation=\\\"clearspeak:simple\\\" data-semantic-children=\\\"4\\\" data-semantic-content=\\\"3\\\" data-semantic- data-semantic-parent=\\\"6\\\" data-semantic-role=\\\"negative\\\" data-semantic-type=\\\"prefixop\\\" size=\\\"s\\\"><mjx-mo data-semantic- data-semantic-operator=\\\"prefixop,−\\\" data-semantic-parent=\\\"5\\\" data-semantic-role=\\\"subtraction\\\" data-semantic-type=\\\"operator\\\" rspace=\\\"1\\\"><mjx-c></mjx-c></mjx-mo><mjx-mn data-semantic-annotation=\\\"clearspeak:simple\\\" data-semantic-font=\\\"normal\\\" data-semantic- data-semantic-parent=\\\"5\\\" data-semantic-role=\\\"float\\\" data-semantic-type=\\\"number\\\"><mjx-c></mjx-c><mjx-c></mjx-c><mjx-c></mjx-c></mjx-mn></mjx-mrow></mjx-script></mjx-msup></mjx-mrow></mjx-semantics></mjx-math><mjx-assistive-mml display=\\\"inline\\\" unselectable=\\\"on\\\"><math altimg=\\\"urn:x-wiley:25130390:media:adts70009:adts70009-math-0009\\\" display=\\\"inline\\\" location=\\\"graphic/adts70009-math-0009.png\\\" xmlns=\\\"http://www.w3.org/1998/Math/MathML\\\"><semantics><mrow data-semantic-=\\\"\\\" data-semantic-children=\\\"6\\\" data-semantic-content=\\\"0\\\" data-semantic-role=\\\"unknown\\\" data-semantic-speech=\\\"times 10 Superscript negative 0.7\\\" data-semantic-type=\\\"prefixop\\\"><mo data-semantic-=\\\"\\\" data-semantic-operator=\\\"prefixop,×\\\" data-semantic-parent=\\\"7\\\" data-semantic-role=\\\"unknown\\\" data-semantic-type=\\\"operator\\\">×</mo><mspace width=\\\"0.33em\\\"></mspace><msup data-semantic-=\\\"\\\" data-semantic-children=\\\"2,5\\\" data-semantic-parent=\\\"7\\\" data-semantic-role=\\\"integer\\\" data-semantic-type=\\\"superscript\\\"><mn data-semantic-=\\\"\\\" data-semantic-annotation=\\\"clearspeak:simple\\\" data-semantic-font=\\\"normal\\\" data-semantic-parent=\\\"6\\\" data-semantic-role=\\\"integer\\\" data-semantic-type=\\\"number\\\">10</mn><mrow data-semantic-=\\\"\\\" data-semantic-annotation=\\\"clearspeak:simple\\\" data-semantic-children=\\\"4\\\" data-semantic-content=\\\"3\\\" data-semantic-parent=\\\"6\\\" data-semantic-role=\\\"negative\\\" data-semantic-type=\\\"prefixop\\\"><mo data-semantic-=\\\"\\\" data-semantic-operator=\\\"prefixop,−\\\" data-semantic-parent=\\\"5\\\" data-semantic-role=\\\"subtraction\\\" data-semantic-type=\\\"operator\\\">−</mo><mn data-semantic-=\\\"\\\" data-semantic-annotation=\\\"clearspeak:simple\\\" data-semantic-font=\\\"normal\\\" data-semantic-parent=\\\"5\\\" data-semantic-role=\\\"float\\\" data-semantic-type=\\\"number\\\">0.7</mn></mrow></msup></mrow>$ \\\\times\\\\ {10^{ - 0.7}}$</annotation></semantics></math></mjx-assistive-mml></mjx-container> and 5.5421 <span data-altimg=\\\"/cms/asset/0c3733e9-a252-4030-b6fc-8be41093d005/adts70009-math-0010.png\\\"></span><mjx-container ctxtmenu_counter=\\\"19\\\" ctxtmenu_oldtabindex=\\\"1\\\" jax=\\\"CHTML\\\" role=\\\"application\\\" sre-explorer- style=\\\"font-size: 103%; position: relative;\\\" tabindex=\\\"0\\\"><mjx-math aria-hidden=\\\"true\\\" location=\\\"graphic/adts70009-math-0010.png\\\"><mjx-semantics><mjx-mrow data-semantic-children=\\\"6\\\" data-semantic-content=\\\"0\\\" data-semantic- data-semantic-role=\\\"unknown\\\" data-semantic-speech=\\\"times 10 Superscript negative 0.7\\\" data-semantic-type=\\\"prefixop\\\"><mjx-mo data-semantic- data-semantic-operator=\\\"prefixop,×\\\" data-semantic-parent=\\\"7\\\" data-semantic-role=\\\"unknown\\\" data-semantic-type=\\\"operator\\\" rspace=\\\"4\\\" space=\\\"4\\\"><mjx-c></mjx-c></mjx-mo><mjx-mspace style=\\\"width: 0.33em;\\\"></mjx-mspace><mjx-msup data-semantic-children=\\\"2,5\\\" data-semantic- data-semantic-parent=\\\"7\\\" data-semantic-role=\\\"integer\\\" data-semantic-type=\\\"superscript\\\"><mjx-mn data-semantic-annotation=\\\"clearspeak:simple\\\" data-semantic-font=\\\"normal\\\" data-semantic- data-semantic-parent=\\\"6\\\" data-semantic-role=\\\"integer\\\" data-semantic-type=\\\"number\\\"><mjx-c></mjx-c><mjx-c></mjx-c></mjx-mn><mjx-script style=\\\"vertical-align: 0.393em;\\\"><mjx-mrow data-semantic-annotation=\\\"clearspeak:simple\\\" data-semantic-children=\\\"4\\\" data-semantic-content=\\\"3\\\" data-semantic- data-semantic-parent=\\\"6\\\" data-semantic-role=\\\"negative\\\" data-semantic-type=\\\"prefixop\\\" size=\\\"s\\\"><mjx-mo data-semantic- data-semantic-operator=\\\"prefixop,−\\\" data-semantic-parent=\\\"5\\\" data-semantic-role=\\\"subtraction\\\" data-semantic-type=\\\"operator\\\" rspace=\\\"1\\\"><mjx-c></mjx-c></mjx-mo><mjx-mn data-semantic-annotation=\\\"clearspeak:simple\\\" data-semantic-font=\\\"normal\\\" data-semantic- data-semantic-parent=\\\"5\\\" data-semantic-role=\\\"float\\\" data-semantic-type=\\\"number\\\"><mjx-c></mjx-c><mjx-c></mjx-c><mjx-c></mjx-c></mjx-mn></mjx-mrow></mjx-script></mjx-msup></mjx-mrow></mjx-semantics></mjx-math><mjx-assistive-mml display=\\\"inline\\\" unselectable=\\\"on\\\"><math altimg=\\\"urn:x-wiley:25130390:media:adts70009:adts70009-math-0010\\\" display=\\\"inline\\\" location=\\\"graphic/adts70009-math-0010.png\\\" xmlns=\\\"http://www.w3.org/1998/Math/MathML\\\"><semantics><mrow data-semantic-=\\\"\\\" data-semantic-children=\\\"6\\\" data-semantic-content=\\\"0\\\" data-semantic-role=\\\"unknown\\\" data-semantic-speech=\\\"times 10 Superscript negative 0.7\\\" data-semantic-type=\\\"prefixop\\\"><mo data-semantic-=\\\"\\\" data-semantic-operator=\\\"prefixop,×\\\" data-semantic-parent=\\\"7\\\" data-semantic-role=\\\"unknown\\\" data-semantic-type=\\\"operator\\\">×</mo><mspace width=\\\"0.33em\\\"></mspace><msup data-semantic-=\\\"\\\" data-semantic-children=\\\"2,5\\\" data-semantic-parent=\\\"7\\\" data-semantic-role=\\\"integer\\\" data-semantic-type=\\\"superscript\\\"><mn data-semantic-=\\\"\\\" data-semantic-annotation=\\\"clearspeak:simple\\\" data-semantic-font=\\\"normal\\\" data-semantic-parent=\\\"6\\\" data-semantic-role=\\\"integer\\\" data-semantic-type=\\\"number\\\">10</mn><mrow data-semantic-=\\\"\\\" data-semantic-annotation=\\\"clearspeak:simple\\\" data-semantic-children=\\\"4\\\" data-semantic-content=\\\"3\\\" data-semantic-parent=\\\"6\\\" data-semantic-role=\\\"negative\\\" data-semantic-type=\\\"prefixop\\\"><mo data-semantic-=\\\"\\\" data-semantic-operator=\\\"prefixop,−\\\" data-semantic-parent=\\\"5\\\" data-semantic-role=\\\"subtraction\\\" data-semantic-type=\\\"operator\\\">−</mo><mn data-semantic-=\\\"\\\" data-semantic-annotation=\\\"clearspeak:simple\\\" data-semantic-font=\\\"normal\\\" data-semantic-parent=\\\"5\\\" data-semantic-role=\\\"float\\\" data-semantic-type=\\\"number\\\">0.7</mn></mrow></msup></mrow>$ \\\\times\\\\ {10^{ - 0.7}}$</annotation></semantics></math></mjx-assistive-mml></mjx-container>, respectively. The hybrid nanofluid flows over the Riga plate has numerous applications in mechanical engineering, including fuel systems, magnetohydrodynamic (MHD) pumps, energy systems, thermal reactors, etc.\",\"PeriodicalId\":7219,\"journal\":{\"name\":\"Advanced Theory and Simulations\",\"volume\":\"45 1\",\"pages\":\"\"},\"PeriodicalIF\":2.9000,\"publicationDate\":\"2025-05-20\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"\",\"citationCount\":\"0\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Advanced Theory and Simulations\",\"FirstCategoryId\":\"5\",\"ListUrlMain\":\"https://doi.org/10.1002/adts.202500352\",\"RegionNum\":4,\"RegionCategory\":\"工程技术\",\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"\",\"PubModel\":\"\",\"JCR\":\"Q1\",\"JCRName\":\"MULTIDISCIPLINARY SCIENCES\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Advanced Theory and Simulations","FirstCategoryId":"5","ListUrlMain":"https://doi.org/10.1002/adts.202500352","RegionNum":4,"RegionCategory":"工程技术","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q1","JCRName":"MULTIDISCIPLINARY SCIENCES","Score":null,"Total":0}
引用次数: 0
摘要
在考虑辐射、指数热源、粘性耗散、磁场和活化能等影响因素的情况下,研究化学反应型和磁矿型混合纳米流体(由A ^ l2 ^ O3/Cu${\mathrm{A}}{{\mathrm{l}}_{2}}{{\mathrm{O}}_3}/{\mathrm{O}}$组成)在Riga板上的热扩散和质量扩散特性。利用相似变换将控制方程转化为常微分方程,利用MATLAB中的bvp4c求解器对微分方程进行求解,得到数值解。无量纲参数范围0.1 <;Z & lt;1,0 <;Kp & lt;0.5, 1 <;R & lt;5.0.1 <;Ec & lt;0.4, 0.1 <;φ1${\varphi _1}$ <;0.4, 0.1 <;φ2${\varphi _2}$ <;0.4, 0.1 <;量化宽松政策$ {Q_E} $ & lt;0.4, 0.1 <;Bi & lt;0.4, 1 <;ex $ R {e_x} $ & lt;5、0.1 <;𝛾& lt;0.7. 温度分布随哈特曼数和辐射的增大而增大,速度分布随修正哈特曼数的增大而增大。随着活化能的提高,浓度曲线也随之增强。努塞尔数随着指数热源的增大而增大,数值QE${Q_{\mathrm{E}}}$ = 0.2, QE${Q_{\mathrm{E}}}$ = 0.3。对应的努塞尔数分别为2.8232 ×10−0.7$ \times\{10^{- 0.7}}$和5.5421 ×10−0.7$ \times\{10^{- 0.7}}$。在里加板上流动的混合纳米流体在机械工程中有许多应用,包括燃料系统、磁流体动力(MHD)泵、能源系统、热反应堆等。本文章由计算机程序翻译,如有差异,请以英文原文为准。
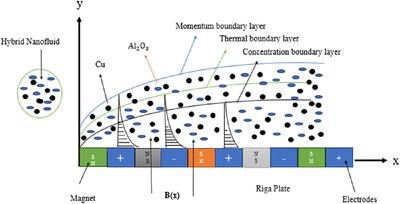
Numerical Investigation of Thermal and Mass Diffusion Characteristics in Chemically Reactive and Magnetite Cu–Al2O3 Water-Based Hybrid Nanofluid Flow over Riga Plate
The existing work intends to explore the thermal and mass diffusion properties in chemically reactive and magnetite hybrid nanofluids (consisting of
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊

Advanced Theory and Simulations
Multidisciplinary-Multidisciplinary
CiteScore
5.50
自引率
3.00%
发文量
221
期刊介绍:
Advanced Theory and Simulations is an interdisciplinary, international, English-language journal that publishes high-quality scientific results focusing on the development and application of theoretical methods, modeling and simulation approaches in all natural science and medicine areas, including:
materials, chemistry, condensed matter physics
engineering, energy
life science, biology, medicine
atmospheric/environmental science, climate science
planetary science, astronomy, cosmology
method development, numerical methods, statistics
×
引用
GB/T 7714-2015
复制
MLA
复制
APA
复制
导出至
BibTeX
EndNote
RefMan
NoteFirst
NoteExpress
请完成安全验证×
微信好友
朋友圈
QQ好友
复制链接
取消

已复制链接
快去分享给好友吧!
我知道了

点击右上角分享
相关文献
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:
