全纯映射到超二次曲面的横向性。

IF 1.3 2区数学 Q1 MATHEMATICS

Mathematische Annalen Pub Date : 2025-01-01 Epub Date: 2025-03-26 DOI:10.1007/s00208-025-03134-5

Xiaojun Huang, Weixia Zhu

{"title":"全纯映射到超二次曲面的横向性。","authors":"Xiaojun Huang, Weixia Zhu","doi":"10.1007/s00208-025-03134-5","DOIUrl":null,"url":null,"abstract":"We study holomorphic maps F from a smooth Levi non-degenerate real hypersurface <math> <mrow><msub><mi>M</mi> <mi>ℓ</mi></msub> <mo>⊂</mo> <msup><mrow><mi>C</mi></mrow> <mi>n</mi></msup> </mrow> </math> into a hyperquadric <math><msubsup><mi>H</mi> <mrow><msup><mi>ℓ</mi> <mo>'</mo></msup> </mrow> <mi>N</mi></msubsup> </math> with signatures <math><mrow><mi>ℓ</mi> <mo>≤</mo> <mo>(</mo> <mi>n</mi> <mo>-</mo> <mn>1</mn> <mo>)</mo> <mo>/</mo> <mn>2</mn></mrow> </math> and <math> <mrow><msup><mi>ℓ</mi> <mo>'</mo></msup> <mo>≤</mo> <mrow><mo>(</mo> <mi>N</mi> <mo>-</mo> <mn>1</mn> <mo>)</mo></mrow> <mo>/</mo> <mn>2</mn> <mo>,</mo></mrow> </math> respectively. Assuming that <math><mrow><mi>N</mi> <mo>-</mo> <mi>n</mi> <mo><</mo> <mi>n</mi> <mo>-</mo> <mn>1</mn> <mo>,</mo></mrow> </math> we prove that if <math><mrow><mi>ℓ</mi> <mo>=</mo> <msup><mi>ℓ</mi> <mo>'</mo></msup> <mo>,</mo></mrow> </math> then F is either CR transversal to <math><msubsup><mi>H</mi> <mrow><mi>ℓ</mi></mrow> <mi>N</mi></msubsup> </math> at every point of <math> <mrow><msub><mi>M</mi> <mi>ℓ</mi></msub> <mo>,</mo></mrow> </math> or it maps a neighborhood of <math><msub><mi>M</mi> <mi>ℓ</mi></msub> </math> in <math> <msup><mrow><mi>C</mi></mrow> <mi>n</mi></msup> </math> into <math> <mrow><msubsup><mi>H</mi> <mrow><mi>ℓ</mi></mrow> <mi>N</mi></msubsup> <mo>.</mo></mrow> </math> Furthermore, in the case where <math> <mrow><msup><mi>ℓ</mi> <mo>'</mo></msup> <mo>></mo> <mi>ℓ</mi> <mo>,</mo></mrow> </math> we show that if F is not CR transversal at <math><mrow><mn>0</mn> <mo>∈</mo> <msub><mi>M</mi> <mi>ℓ</mi></msub> <mo>,</mo></mrow> </math> then it must be transversally flat. The latter is best possible.","PeriodicalId":18304,"journal":{"name":"Mathematische Annalen","volume":"392 2","pages":"1731-1746"},"PeriodicalIF":1.3000,"publicationDate":"2025-01-01","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"https://www.ncbi.nlm.nih.gov/pmc/articles/PMC12084281/pdf/","citationCount":"0","resultStr":"{\"title\":\"Transversality of holomorphic maps into hyperquadrics.\",\"authors\":\"Xiaojun Huang, Weixia Zhu\",\"doi\":\"10.1007/s00208-025-03134-5\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"We study holomorphic maps F from a smooth Levi non-degenerate real hypersurface <math> <mrow><msub><mi>M</mi> <mi>ℓ</mi></msub> <mo>⊂</mo> <msup><mrow><mi>C</mi></mrow> <mi>n</mi></msup> </mrow> </math> into a hyperquadric <math><msubsup><mi>H</mi> <mrow><msup><mi>ℓ</mi> <mo>'</mo></msup> </mrow> <mi>N</mi></msubsup> </math> with signatures <math><mrow><mi>ℓ</mi> <mo>≤</mo> <mo>(</mo> <mi>n</mi> <mo>-</mo> <mn>1</mn> <mo>)</mo> <mo>/</mo> <mn>2</mn></mrow> </math> and <math> <mrow><msup><mi>ℓ</mi> <mo>'</mo></msup> <mo>≤</mo> <mrow><mo>(</mo> <mi>N</mi> <mo>-</mo> <mn>1</mn> <mo>)</mo></mrow> <mo>/</mo> <mn>2</mn> <mo>,</mo></mrow> </math> respectively. Assuming that <math><mrow><mi>N</mi> <mo>-</mo> <mi>n</mi> <mo><</mo> <mi>n</mi> <mo>-</mo> <mn>1</mn> <mo>,</mo></mrow> </math> we prove that if <math><mrow><mi>ℓ</mi> <mo>=</mo> <msup><mi>ℓ</mi> <mo>'</mo></msup> <mo>,</mo></mrow> </math> then F is either CR transversal to <math><msubsup><mi>H</mi> <mrow><mi>ℓ</mi></mrow> <mi>N</mi></msubsup> </math> at every point of <math> <mrow><msub><mi>M</mi> <mi>ℓ</mi></msub> <mo>,</mo></mrow> </math> or it maps a neighborhood of <math><msub><mi>M</mi> <mi>ℓ</mi></msub> </math> in <math> <msup><mrow><mi>C</mi></mrow> <mi>n</mi></msup> </math> into <math> <mrow><msubsup><mi>H</mi> <mrow><mi>ℓ</mi></mrow> <mi>N</mi></msubsup> <mo>.</mo></mrow> </math> Furthermore, in the case where <math> <mrow><msup><mi>ℓ</mi> <mo>'</mo></msup> <mo>></mo> <mi>ℓ</mi> <mo>,</mo></mrow> </math> we show that if F is not CR transversal at <math><mrow><mn>0</mn> <mo>∈</mo> <msub><mi>M</mi> <mi>ℓ</mi></msub> <mo>,</mo></mrow> </math> then it must be transversally flat. The latter is best possible.\",\"PeriodicalId\":18304,\"journal\":{\"name\":\"Mathematische Annalen\",\"volume\":\"392 2\",\"pages\":\"1731-1746\"},\"PeriodicalIF\":1.3000,\"publicationDate\":\"2025-01-01\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"https://www.ncbi.nlm.nih.gov/pmc/articles/PMC12084281/pdf/\",\"citationCount\":\"0\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Mathematische Annalen\",\"FirstCategoryId\":\"100\",\"ListUrlMain\":\"https://doi.org/10.1007/s00208-025-03134-5\",\"RegionNum\":2,\"RegionCategory\":\"数学\",\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"2025/3/26 0:00:00\",\"PubModel\":\"Epub\",\"JCR\":\"Q1\",\"JCRName\":\"MATHEMATICS\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Mathematische Annalen","FirstCategoryId":"100","ListUrlMain":"https://doi.org/10.1007/s00208-025-03134-5","RegionNum":2,"RegionCategory":"数学","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"2025/3/26 0:00:00","PubModel":"Epub","JCR":"Q1","JCRName":"MATHEMATICS","Score":null,"Total":0}

引用次数: 0

摘要

研究了从光滑Levi非简并实超曲面M∧C n到签名分别为r≤(n- 1) / 2和r′≤(n- 1) / 2的超二次曲面H∧n的全纯映射F。假设N - N - N - 1，我们证明了如果N = N '，那么F要么在M l的每一点上都是CR截于H l N，要么它将C N中M l的一个邻域映射到H l N。进一步地，我们证明了如果F在0∈M r处不是CR横截，那么它一定是横截平的。后者是最好的选择。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

查看原文本刊更多论文

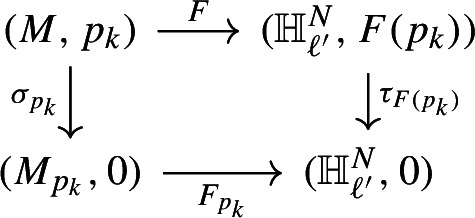
Transversality of holomorphic maps into hyperquadrics.

We study holomorphic maps F from a smooth Levi non-degenerate real hypersurface $M_{ℓ} \subset C^{n}$ into a hyperquadric $H_{ℓ^{'}}^{N}$ with signatures $ℓ \leq (n - 1) / 2$ and $ℓ^{'} \leq (N - 1) / 2,$ respectively. Assuming that $N - n < n - 1,$ we prove that if $ℓ = ℓ^{'},$ then F is either CR transversal to $H_{ℓ}^{N}$ at every point of $M_{ℓ},$ or it maps a neighborhood of $M_{ℓ}$ in $C^{n}$ into $H_{ℓ}^{N} .$ Furthermore, in the case where $ℓ^{'} > ℓ,$ we show that if F is not CR transversal at $0 \in M_{ℓ},$ then it must be transversally flat. The latter is best possible.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Mathematische Annalen 数学-数学

CiteScore

2.90

自引率

7.10%

发文量

181

审稿时长

4-8 weeks

期刊介绍： Begründet 1868 durch Alfred Clebsch und Carl Neumann. Fortgeführt durch Felix Klein, David Hilbert, Otto Blumenthal, Erich Hecke, Heinrich Behnke, Hans Grauert, Heinz Bauer, Herbert Amann, Jean-Pierre Bourguignon, Wolfgang Lück und Nigel Hitchin. The journal Mathematische Annalen was founded in 1868 by Alfred Clebsch and Carl Neumann. It was continued by Felix Klein, David Hilbert, Otto Blumenthal, Erich Hecke, Heinrich Behnke, Hans Grauert, Heinz Bauer, Herbert Amann, Jean-Pierre Bourguigon, Wolfgang Lück and Nigel Hitchin. Since 1868 the name Mathematische Annalen stands for a long tradition and high quality in the publication of mathematical research articles. Mathematische Annalen is designed not as a specialized journal but covers a wide spectrum of modern mathematics.