稀疏高斯过程中有限元逼近诱导点的自动选择
IF 8
2区 计算机科学
Q1 AUTOMATION & CONTROL SYSTEMS
Engineering Applications of Artificial Intelligence
Pub Date : 2025-03-31
DOI:10.1016/j.engappai.2025.110629
引用次数: 0
摘要
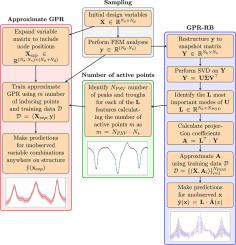
高斯过程回归(GPR)是一种应用广泛的回归模型,但其可扩展性较差。稀疏逼近方法通过使用诱导点来近似GPR来提高可伸缩性,但是确定这些点的最佳数量和位置是具有挑战性的。增加诱导点的数量通常可以提高预测精度,但这需要计算成本。本文提出了一种利用近似探地雷达估计有限元法(FEM)分析准确预测所需诱导点数目的方法。该方法利用适当的正交分解(POD)技术,利用其模式来确定诱导点。结果表明,该方法识别了足够数量的近似GPR诱导点,达到了与全GPR相当的预测精度,但训练时间只有全GPR的一半。这种方法在保证计算效率的同时,又不影响计算精度,使其成为工程应用中可扩展回归的重要工具。POD先前已与GPR相结合,通过简化基函数分别处理空间分量,为未见变量组合的完整解决方案提供计算效率预测。然而,这项工作将空间分量视为GPR近似中的一个变量,从而允许连续的空间预测。这确保了空间维度上的协方差被单个GPR捕获。将该方法应用于某三跨后张式混凝土梁桥的结构仿真。本文章由计算机程序翻译,如有差异,请以英文原文为准。
Automatic selection of inducing points in sparse Gaussian process for approximations of finite element analyses
Gaussian process regression (GPR) is a widely used regression model, but it has poor scalability. Sparse approximation methods improve scalability by using inducing points to approximate the GPR, but determining the optimal number and placement of these points is challenging. Increasing the number of inducing points generally improves the predictive accuracy, but it comes at a computational cost. This article presents a method to estimate the necessary number of inducing points for accurate predictions of finite element method (FEM) analyses using approximate GPR. The approach leverages the proper orthogonal decomposition (POD) technique, using its modes to determine the inducing points. Results demonstrate that the proposed method identifies a sufficient number of inducing points for approximate GPR to achieve predictive accuracy comparable to full GPR, but with half the training time. This approach ensures computational efficiency without significant loss in accuracy, making it a valuable tool for scalable regression in engineering applications. POD has previously been combined with GPR to provide computationally efficient predictions for the full solution field across unseen variable combinations, treating spatial components separately via reduced basis functions. However, this work treats the spatial component as a variable within the GPR approximation, allowing continuous spatial predictions. This ensures that the covariance in the spatial dimension is captured by a single GPR. The method is applied to simulations of a three-span, post-tensioned concrete girder bridge.
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊

Engineering Applications of Artificial Intelligence
工程技术-工程:电子与电气
CiteScore
9.60
自引率
10.00%
发文量
505
审稿时长
68 days
期刊介绍:
Artificial Intelligence (AI) is pivotal in driving the fourth industrial revolution, witnessing remarkable advancements across various machine learning methodologies. AI techniques have become indispensable tools for practicing engineers, enabling them to tackle previously insurmountable challenges. Engineering Applications of Artificial Intelligence serves as a global platform for the swift dissemination of research elucidating the practical application of AI methods across all engineering disciplines. Submitted papers are expected to present novel aspects of AI utilized in real-world engineering applications, validated using publicly available datasets to ensure the replicability of research outcomes. Join us in exploring the transformative potential of AI in engineering.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


