变形Wigner矩阵的Loschmidt回波。

IF 1.3 3区物理与天体物理 Q3 PHYSICS, MATHEMATICAL

Letters in Mathematical Physics Pub Date : 2025-01-30 DOI:10.1007/s11005-025-01904-5

László Erdős, Joscha Henheik, Oleksii Kolupaiev

{"title":"变形Wigner矩阵的Loschmidt回波。","authors":"László Erdős, Joscha Henheik, Oleksii Kolupaiev","doi":"10.1007/s11005-025-01904-5","DOIUrl":null,"url":null,"abstract":"<div>We consider two Hamiltonians that are close to each other, \\(H_1 \\approx H_2 \\), and analyze the time decay of the corresponding Loschmidt echo \\(\\mathfrak {M}(t):= |\\langle \\psi _0, \\textrm{e}^{\\textrm{i} t H_2} \\textrm{e}^{-\\textrm{i} t H_1} \\psi _0 \\rangle |^2\\) that expresses the effect of an imperfect time reversal on the initial state \\(\\psi _0\\). Our model Hamiltonians are deformed Wigner matrices that do not share a common eigenbasis. The main tools are new two-resolvent laws for such \\(H_1\\) and \\(H_2\\).</div>","PeriodicalId":685,"journal":{"name":"Letters in Mathematical Physics","volume":"115 1","pages":""},"PeriodicalIF":1.3000,"publicationDate":"2025-01-30","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"https://www.ncbi.nlm.nih.gov/pmc/articles/PMC11782466/pdf/","citationCount":"0","resultStr":"{\"title\":\"Loschmidt echo for deformed Wigner matrices\",\"authors\":\"László Erdős, Joscha Henheik, Oleksii Kolupaiev\",\"doi\":\"10.1007/s11005-025-01904-5\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"<div>We consider two Hamiltonians that are close to each other, \\\\(H_1 \\\\approx H_2 \\\\), and analyze the time decay of the corresponding Loschmidt echo \\\\(\\\\mathfrak {M}(t):= |\\\\langle \\\\psi _0, \\\\textrm{e}^{\\\\textrm{i} t H_2} \\\\textrm{e}^{-\\\\textrm{i} t H_1} \\\\psi _0 \\\\rangle |^2\\\\) that expresses the effect of an imperfect time reversal on the initial state \\\\(\\\\psi _0\\\\). Our model Hamiltonians are deformed Wigner matrices that do not share a common eigenbasis. The main tools are new two-resolvent laws for such \\\\(H_1\\\\) and \\\\(H_2\\\\).</div>\",\"PeriodicalId\":685,\"journal\":{\"name\":\"Letters in Mathematical Physics\",\"volume\":\"115 1\",\"pages\":\"\"},\"PeriodicalIF\":1.3000,\"publicationDate\":\"2025-01-30\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"https://www.ncbi.nlm.nih.gov/pmc/articles/PMC11782466/pdf/\",\"citationCount\":\"0\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Letters in Mathematical Physics\",\"FirstCategoryId\":\"101\",\"ListUrlMain\":\"https://link.springer.com/article/10.1007/s11005-025-01904-5\",\"RegionNum\":3,\"RegionCategory\":\"物理与天体物理\",\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"\",\"PubModel\":\"\",\"JCR\":\"Q3\",\"JCRName\":\"PHYSICS, MATHEMATICAL\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Letters in Mathematical Physics","FirstCategoryId":"101","ListUrlMain":"https://link.springer.com/article/10.1007/s11005-025-01904-5","RegionNum":3,"RegionCategory":"物理与天体物理","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q3","JCRName":"PHYSICS, MATHEMATICAL","Score":null,"Total":0}

引用次数: 0

摘要

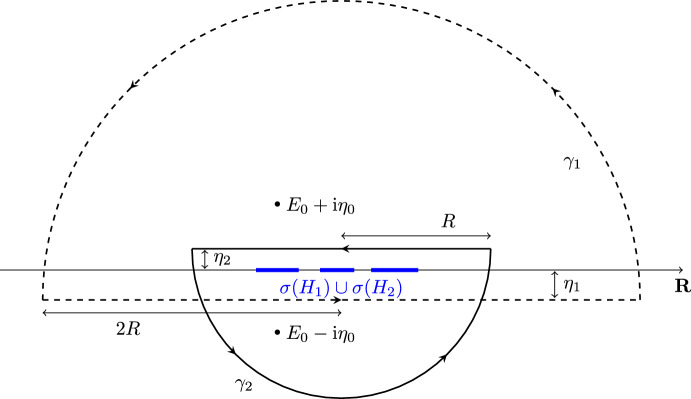
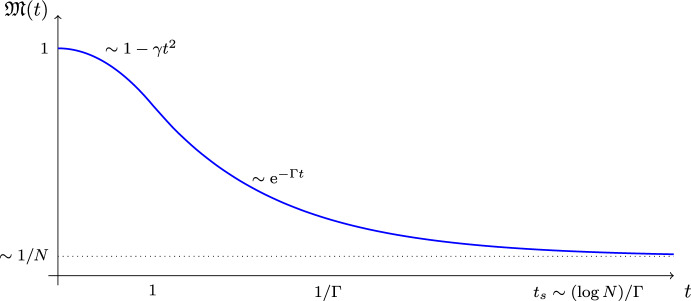
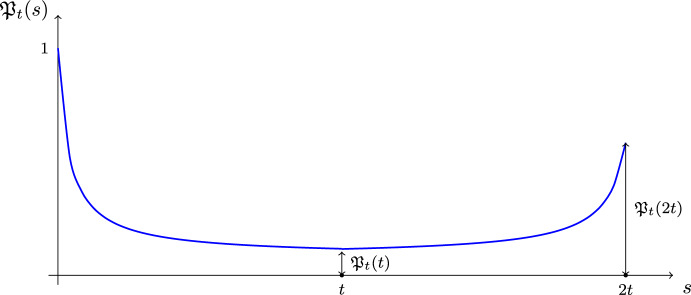
我们考虑两个彼此接近的哈密顿量，H 1≈H 2，并分析相应的洛施密特回波M (t)的时间衰减：= |⟨ψ 0, e it H 2 e - i i H 1 ψ 0⟩| 2，它表示不完全时间反转对初始状态ψ 0的影响。我们的模型哈密顿矩阵是不具有共同特征基的变形维格纳矩阵。主要的工具是关于h1和h2的新的双分解定律。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

查看原文本刊更多论文

Loschmidt echo for deformed Wigner matrices

We consider two Hamiltonians that are close to each other, \(H_1 \approx H_2 \), and analyze the time decay of the corresponding Loschmidt echo \(\mathfrak {M}(t):= |\langle \psi _0, \textrm{e}^{\textrm{i} t H_2} \textrm{e}^{-\textrm{i} t H_1} \psi _0 \rangle |^2\) that expresses the effect of an imperfect time reversal on the initial state \(\psi _0\). Our model Hamiltonians are deformed Wigner matrices that do not share a common eigenbasis. The main tools are new two-resolvent laws for such \(H_1\) and \(H_2\).

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Letters in Mathematical Physics 物理-物理：数学物理

CiteScore

2.40

自引率

8.30%

发文量

111

审稿时长

3 months

期刊介绍： The aim of Letters in Mathematical Physics is to attract the community''s attention on important and original developments in the area of mathematical physics and contemporary theoretical physics. The journal publishes letters and longer research articles, occasionally also articles containing topical reviews. We are committed to both fast publication and careful refereeing. In addition, the journal offers important contributions to modern mathematics in fields which have a potential physical application, and important developments in theoretical physics which have potential mathematical impact.