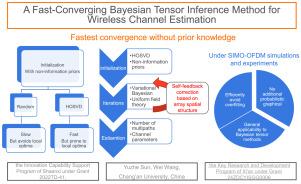
A fast-converging Bayesian tensor inference method for wireless channel estimation

In variational inference-based tensor channel estimation, high order singular value decomposition (HOSVD) initialization effectively captures the latent features of factor matrices, and accelerates convergence speed. However, HOSVD-based initialization further exacerbates the overfitting issue of the tensor variation Bayesian (TVB) method on each factor matrix element, leading to inaccurate rank estimation, and then significantly degrading channel parameter estimation performance. To prevent overfitting, we propose a new TVB method based on array spatial prior (ASP), which incorporates space correlations in tensor data, without introducing additional hierarchical probabilistic models. By analyzing the inferred posterior distribution and the non-decreasing property of the evidence lower bound (ELBO), we confirm the favorable convergence characteristics and global search capability of the proposed algorithm. Through simulations and experiments, we observe that compared to traditional TVB, the proposed algorithm achieves accurate automatic rank determination (ARD) in just a few iterations, significantly reducing convergence time. Meanwhile, it demonstrates superior parameter estimation accuracy with fewer iterations than the compared method.